Einführung in die digitale Signalverarbeitung Teil 7/8
Aus ELVjournal
02/2008
0 Kommentare
Die schnelle Fouriertransformation
Die
schnelle Fouriertransformation (FFT: Fast Fourier Transform) ist ein
Algorithmus, mit dem sich eine diskrete Fouriertransformation (DFT)
erheblich schneller durchführen lässt. Am bekanntesten sind die
Radix-2-FFT-Algorithmen, die der deutsche Mathematiker Carl Friedrich
Gauß schon um 1805 für die Berechnung von Asteroidenbahnen entwarf.
James W. Cooley and John W. Tukey stellten den Radix-2- Algorithmus 1965
in dem Aufsatz „An algorithm for the machine calculation of complex
Fourier series“ in Mathematics of Computation 19, 297–301 (1965), für
die „maschinelle Berechnung komplexer Fourierreihen“ vor. Dabei wird die
zu transformierende Folge – deren Länge N eine Potenz zur Basis 2 ist –
entweder im Zeitbereich (DIT: decimation in time) oder im
Frequenzbereich (DIF: decimation in frequency) so lange zerlegt, bis
elementare, einfachst zu berechnende Strukturen – die Butterflys
(Schmetterlinge) – entstehen. Bei der Herleitung der Algorithmen durch
diese Teile-und-herrsche-Strategie spielen die Symmetrieeigenschaften
des Drehfaktors W eine wichtige Rolle.FFT durch Dezimierung im Zeitbereich
Wir
gehen von der Definitionsgleichung 85 der DFT aus (s. Gleichung 90).
Sie transformiert eine Folge von N Werten im Zeitbereich in N
Frequenzwerte. Wenn die Voraussetzung erfüllt ist, dass die Anzahl der
Zeitfolgenwerte x(n) eine Potenz von zwei ist (also N = 4, 8, 16, 32, 64
…), dann ist eine Aufspaltung von x(n) in zwei Teilfolgen g(n) mit
geraden und u(n) mit ungeraden Indizes möglich (Gleichung 91).Damit
lässt sich Gleichung 90 umschreiben als Gleichung 92. Nun machen wir
uns zunutze, dass Gleichung 93 gilt. Zum Verständnis von Gleichung 93
wollen wir den darin ausgedrückten Zusammenhang in Gleichung 94 einmal
ableiten. Dabei nutzen wir die Definition des Drehfaktors aus Gleichung
88. Nun
setzen wir Gleichung 94 in Gleichung 92 ein und erhalten Gleichung 95.
Die Summenterme sind nun nichts weiter als die Fouriertransformierten
der N/2 langen Teilfolgen mit den geraden und ungeraden Indizes. Wenn
wir die Fouriertransformierte von g(n) als G(k) bezeichnen und die von
u(n) als U(k) geht Gleichung 95 in Gleichung 96 über. Nun
könnte man die Richtigkeit von Gleichung 96 anzweifeln, weil G(k) und
U(k) ja jeweils nur N/2 Punkte aufweisen. Aber wegen der Periodizität
der komplexen Exponentialausdrücke kann man Gleichung 97 schreiben.
Wegen Gleichung 97 gilt Gleichung 96 für alle k, also 0 ≤ k ≤ N–1.
Gleichung 96 ließe sich nun direkt in ein Blockschaltbild umsetzen.
Zuvor wollen wir uns aber eine Vereinfachung zunutze machen, die sich
direkt aus Gleichung 96 ableiten lässt. Betrachten wir X(k) und X(k +
N/2) entsprechend Gleichung 98, die für N = 8 ihre direkte Entsprechung
in Abbildung 61 findet. 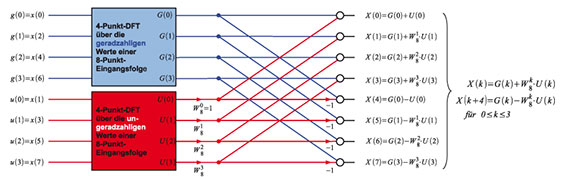
|
| Bild
61: Von der DFT zur FFT: Anstatt eine 8 Werte lange Folge der DFT zu
unterwerfen (8-Punkt-DFT), kann man auch die Werte der Eingangsfolge mit
geradzahligen und ungeradzahligen Indizes transformieren (zwei
4-Punkt-DFTs) und die Ergebnisse verknüpfen. |
Bei
der verwendeten Graphendarstellung wurden die folgenden Vereinbarungen
getroffen. Pfeile stellen Multiplizierer, voll ausgefüllte Punkte
Verzweigungen und Kreise Addierer dar. Der Wert unter einem Pfeil ist
mit dem Signal zu multiplizieren. Ist dieser Wert ein Drehfaktor, so
handelt es sich um eine komplexe Multiplikation, ist er –1, so muss der
Signalwert nur invertiert werden. Wir sehen in Gleichung 98, dass nur
die aus den ungeraden Zeitfolgewerten entstandenen Spektralwerte U(k)
mit den Drehfaktoren (Twiddle Factors) multipliziert werden. Bei den
Ergebnisspektralwerten X(n) mit 0 ≤ n ≤ 3 werden diese Produkte zu den
von den geradzahligen Zeitfolgewerten herrührenden Spektralwerten G(k)
addiert, für X(n) mit 4 ≤ n ≤ 7 wird dagegen die Differenz gebildet.
Weil wir anfangs voraussetzten, dass die Anzahl der Zeitfolgenwerte x(n)
eine Potenz von zwei ist (hier N = 2³ = 8), können wir nun für jeden
der 4-Punkt-DFT-Blöcke deren Eingangsfolge wieder aufspalten, was zu
jeweils zwei 2-Punkt-DFTs führt. Für
G(k) folgt daraus Gleichung 99, die wiederum nichts anderes ist als
eine N/4-Punkt-DFT von g(n) für gerade n und eine mit dem Drehfaktor bewertete N/4-Punkt-DFT von g(n) für ungerade n. Das Ergebnis für den oberen Block in Abbildung 61 unter Berücksichtigung von 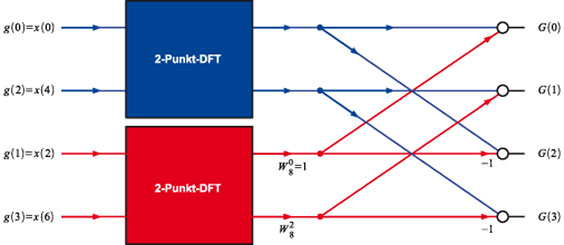
|
| Bild 62: Eine 4-Punkt-DFT wird zu zwei 2-Punkt-DFTs. |
Die
elementaren 2-Punkt-DFTs (im Englischen wegen der Gestalt ihres Graphen
auch Butterflys = Schmetterlinge genannt) werden nun in völliger
Analogie als dritter und letzter Dezimierungsschritt durchgeführt und in
Abbildung 63 dargestellt. 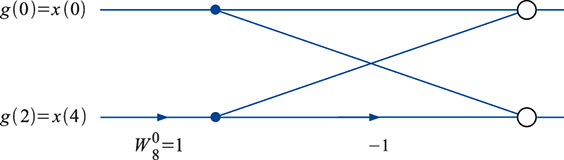
|
| Bild 63: Bei der 2-Punkt-DFT (elementarer Butterfly) ist keine weitere Zerlegung möglich. |
Alle
drei Dezimierungsschritte zusammen zeigt Abbildung 64. Die abgebildete
Struktur benötigt allerdings die Eingangsfolgenwerte in einer
umsortierten Reihenfolge. Dabei wird der Index der Originalfolge als
rückwärts gelesenes Bitmuster (bit reversed binary) zum Index in der
umsortierten Folge. Also z. B. x(4) = x(I00) → x(00I) = x(1), oder x(3) =
x(0II) → x(II0) = x(6). Der erste, dritte, sechste und achte (letzte)
Wert der Zeitfolge bleiben an ihren Plätzen, weil 000, 0I0, I0I und III
vorwärts und rückwärts gelesen den gleichen Wert ergeben. 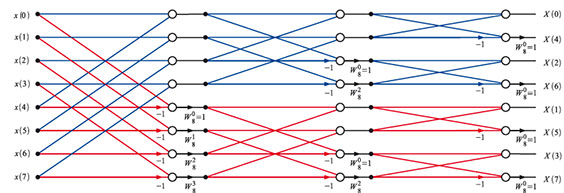
|
| Bild 64: Der vollständig entwickelte DIT-FFT-Signalgraph für 8 Signalpunkte |
FFT durch Dezimierung im Frequenzbereich
Die
fortlaufende Dezimierung der Ausgangs-Frequenzfolge (DIF: decimation in
frequency) in immer kleinere Teilfolgen führt zu ähnlichen Algorithmen,
wie sie die Zerlegung der Zeitfolgen liefert. Wir wollen die Herleitung
nur kurz anreißen, sie geschieht in vollständiger formaler Analogie zur
DIT. Auch hier setzen wir voraus, dass die Länge N der zu zerlegenden
Ausgangsfolge eine Potenz von zwei ist. Wir gehen von der
Definitionsgleichung 85 der DFT aus und bilden die Teilfolgen G(k) aus
den geraden und U(k) aus den ungeraden Werten von X(k) (Gleichung 100).Jetzt
werden G(k) und U(k) jeweils in zwei Summen aufgeteilt, welche die
ersten N/2 und letzten N/2 Punkte enthalten. Zunächst führen wir das in
Gleichung 101 für G(k) durch. U(k) wird wie in Gleichung 102 in
entsprechender Weise zerlegt. Die Gleichungen 101 und 102 lassen sich für N = 8 unmittelbar in einen Graphen gemäß Abbildung 65 umsetzen. 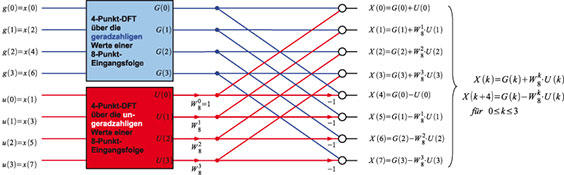
|
| Bild
65: Der FFT-Algorithmus durch fortwährendes Zerlegen der Frequenzfolge
(Decimation in Frequency: DIF) führt zu formal ähnlichen Signalgraphen,
wie sie die Aufspaltung der Zeitfolge (Decimation in Time: DIT) ergibt. |
Nach
einer abermaligen Zerlegung der beiden Frequenzausgangsfolgen verbleibt
als Ergebnis der Graph in Abbildung 66. Man sieht, dass jetzt die
Eingangsfolgenwerte x(n) in natürlicher Reihenfolge vorliegen, die
Ausgangsfolgenwerte X(k) dagegen in eine geänderte Reihenfolge durch
Bitumkehr der Indizes (bit reversal) umzusortieren sind. Bei genauer
Betrachtung sowohl der DIT- als auch der DIF-Signalflussgraphen fällt
auf, dass N Speicherplätze für die Variablen genügen, weil die N
Eingangsgrößen des Graphen x(0), x(1) …, x(n) …, x(N–1) nach der
Verarbeitung in der ersten Berechnungsstufe für den weiteren Verlauf der
Berechnung nicht mehr erforderlich sind. Ihre Speicherplätze können
also zur Zwischenablage der Ausgangsgrößen der ersten Berechnungsstufe
überschrieben und als Eingangsgrößen für die zweite Berechnungsstufe
verwendet werden usw., bis nach vollständiger Durchführung der FFT dort
die Ergebniswerte X(0), X(1) …, X(k) …, X(N–1) stehen. Diese
Vorgehensweise wird als „in place operation“ bezeichnet. 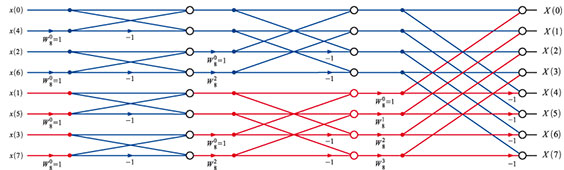
|
| Bild 66: Der vollständig entwickelte DIF-FFT-Signalgraph für 8 Signalpunkte |
Effizienzsteigerung der FFT gegenüber der DFT
Bei
der Berechnung der DFT nach dem Radix-2-Algorithmus ergeben sich
erheblich weniger Berechnungen als bei der direkten Umsetzung der
DFT-Formel. Bei einer Zeitfolgenlänge von N = 2n fallen insgesamt 0,5 • N
• ld(N) komplexe Multiplikationen (ld: logarithmus dualis = Logarithmus
zur Basis 2), N • ld(N) komplexe Additionen und (N/2) • ld(N)
Inversionen an. Betrachtet man nur die Zahl der komplexen
Multiplikationen (die den größten Rechenaufwand darstellen), bei n = 6
(d. h. die Zeitfolge umfasst N = 26 = 64 Werte), erfordert die FFT 0,5 •
64 • 6 = 192 komplexe Multiplikationen im Gegensatz zu N2 = 4096
komplexen Multiplikationen bei der DFT. Der Multiplikationsaufwand der
FFT beträgt also weniger als 5 % desjenigen bei Anwendung der DFT. Diese
Effizienzsteigerung nimmt mit größeren Folgelängen immer weiter zu. Bei
N = 1024 ist der FFT-Multiplikationsaufwand nur ca. 0,49 % im Vergleich
zur DFT. Sogar bei dem Beispiel in Abbildung 64 sind nur 12
Multiplikationen bei der FFT gegenüber 64 bei der DFT durchzuführen. In
der Realität ist die Zahl der Multiplikationen sogar noch etwas
geringer, da alle Drehfaktoren mit Exponent 0 den Wert 1 haben. In Teil 8
dieser Folge beschäftigen wir uns mit den Analyseverfahren für digitale
Abtastsysteme, insbesondere der Darstellung durch
Differenzengleichungen im Zeitbereich und deren z-Transformation in den
Frequenzbereich.Fachbeitrag als PDF-Download herunterladen
Inhalt
Sie erhalten den Artikel in 1 Version:
 als PDF (4 Seiten)
als PDF (4 Seiten)
Sie erhalten folgende Artikel:
- Einführung in die digitale Signalverarbeitung Teil 7/8
| weitere Fachbeiträge | Foren | |
Hinterlassen Sie einen Kommentar:






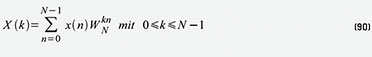
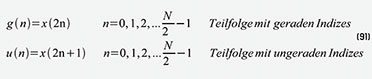
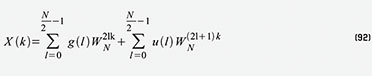

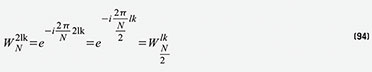
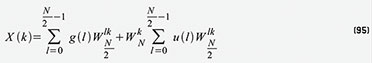


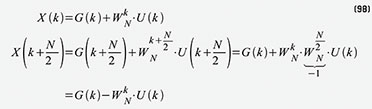

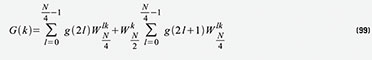
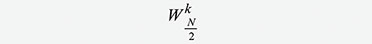



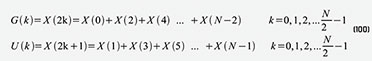
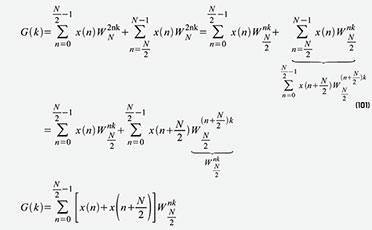



 als PDF (4 Seiten)
als PDF (4 Seiten)