Hallo, Wolfgang SchererLogout
Kontakt
Newsletter
Karriere
 
Sie befinden sich hier: ELVjournal » Journal-Ausgabe 04/2006 » Oszilloskop und Spektrum-Analyzer Teil 1/2 » So funktionierts » Grundlagen/Tabellen/Übersichten

Oszilloskop und Spektrum-Analyzer Teil 1/2

0,00
Aus ELVjournal 04/2006     0 Kommentare
Oszilloskop und Spektrum-Analyzer Teil 1/2

Inhalt des Fachbeitrags

PDF- / Onlineversion herunterladen

Jede Münze hat zwei Seiten! Nur wenn die Beschreibung beider Seiten vorliegt, kann man sich ein vollständiges Bild von ihr machen. Niemand wird an dieser Binsenweisheit zweifeln. Aber ist es genauso klar, dass für jede zeitveränderliche Größe nur deren Charakterisierung im Zeit- und Frequenzbereich das ganze Bild ergibt? Gleichgültig, ob Börsenkurse, seismologische Aktivitäten, das Licht ferner Sterne oder die Erdgeschichte (um nur einige wenige Beispiele zu nennen), stets erschließen sich neue Erkenntnisse, wenn wir über die Beobachtung des zeitlichen Verlaufs einer Größe ihre damit mathematisch verkoppelte Frequenzcharakteristik analysieren. Für Messungen im „Zeitbereich“ (time domain) sind das Oszilloskop und im „Frequenzbereich“ (frequency domain) der Spektrumanalysator die klassischen Hilfsmittel. Mit den Grundlagen der Beschreibung elektrischer Signale und der darauf beruhenden Messtechnik will sich der folgende Artikel beschäftigen.

Zeit-Frequenz-Bezüge

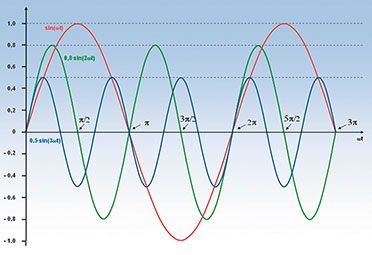
Bild 1: Drei Sinusschwingungen mit unterschiedlicher Frequenz und Amplitude sind die Bestandteile einer komplexeren Schwingung
Bild 1: Drei Sinusschwingungen mit unterschiedlicher Frequenz und Amplitude sind die Bestandteile einer komplexeren Schwingung
Stellen wir uns eine einfache elektrische Sinusschwingung vor. Sie könnte z. B. als Spannung an den Enden einer Leiterschleife entstehen, die mit konstanter Drehzahl in einem konstanten magnetischen Feld rotiert. An diesem Beispiel erkennen wir schon intuitiv, dass zwischen der Drehzahl (Frequenz) und dem Zeitverlauf ein reziproker Zusammenhang besteht. Mit anderen Worten: Je höher die Rotationsfrequenz, umso schneller die zeitliche Änderung der Sinusschwingung. Beschrieben wird das Zeitsignal durch einen Amplitudenverlauf, der eine Funktion der Zeit ist (Abbildung 1). Die rote Kurve beschreibt den sin(ωt). Er ist in 2 π periodisch, d. h. nach einer vollen Umdrehung der Leiterschleife (2 π = 360°) beginnt ein identischer Spannungsabschnitt. Mathematisch drückt sich das darin aus, dass der Sinus bei t = 0, 2 π/ω, 4 π/ω usw. den Wert null annimmt. ω wird auch als Kreisfrequenz bezeichnet und es gilt ω = 2 πf, mit f als Frequenz.
Frequenz f und Zeit t sind also miteinander im Argument der Sinusfunktion verknüpft. Wenn bei der roten Sinuskurve eine volle Sinusschwingung (2 π) nach einer Sekunde durchlaufen ist (Periodendauer 1 s), hat sie eine Frequenz von 1 Hz. Bei der grünen Kurve passen zwei volle Perioden in das Intervall 0 bis 2 π, also hat sie eine Frequenz von 2 Hz, bei der blauen sind es entsprechend 3 Hz. Werden die drei Schwingungen summiert, ergibt sich der Kurvenverlauf aus Abbildung 2. Über einer Frequenzachse werden die drei Sinusschwingungen als senkrechte Striche dargestellt, deren Länge dem Maximalwert der zugehörigen Schwingung (Amplitude) entspricht (Abbildung 3).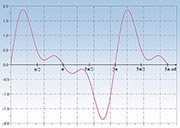
Bild 2: Dies ist die Ergebnisschwingung, wenn man die Schwingungen aus Bild 1 addiert
Bild 2: Dies ist die Ergebnisschwingung, wenn man die Schwingungen aus Bild 1 addiert
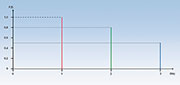
Bild 3: Im Frequenzbereich besteht das Zeitsignal aus Abbildung 2 aus drei Spektrallinien, deren Länge die Amplitude der jeweiligen Frequenzkomponenten darstellt
Bild 3: Im Frequenzbereich besteht das Zeitsignal aus Abbildung 2 aus drei Spektrallinien, deren Länge die Amplitude der jeweiligen Frequenzkomponenten darstellt
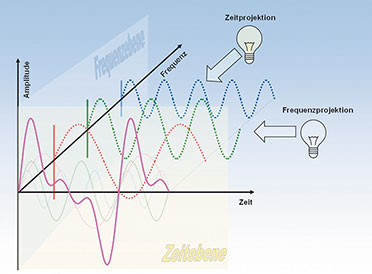
Bild 4: Es ist eine Frage des Standpunktes oder des Blickwinkels, wie sich ein Signal präsentiert, als Zeitfunktion oder als Frequenzspektrum
Bild 4: Es ist eine Frage des Standpunktes oder des Blickwinkels, wie sich ein Signal präsentiert, als Zeitfunktion oder als Frequenzspektrum
In einer dreidimensionalen Darstellung (Abbildung 4) lassen sich die Zusammenhänge weiter veranschaulichen. Die Achsen Zeit, Amplitude und Frequenz spannen einen Raum auf, in den die harmonischen Schwingungen eingezeichnet werden. Sie verlaufen parallel zur Zeitachse und quer zur Frequenzachse. Ist die Zeitprojektionslampe eingeschaltet, werden die Zeitkurven der Harmonischen auf der Zeitebene abgebildet, wo sie sich zum Kurvenzug aus Abbildung 2 überlagern. Mit der Frequenzprojektionslampe dagegen ergibt sich die Abbildung der Harmonischen in Form von drei Strichen auf der Frequenzebene. Ein und derselbe Sachverhalt führt also zu zwei Bildern. Welches der Bilder wir sehen, ist im wahrsten Sinn des Wortes reine Ansichtssache.

Analyse periodischer Zeitsignale

In der Praxis treten aber neben den sinusförmigen auch ganz andere periodische Zeitfunktionen auf: Dreiecke, Rechtecke, Sägezähne usw. Allen ist gemein, dass sie aus der Überlagerung einer Vielzahl von harmonischen Schwingungen (Sinus und Kosinus) mit unterschiedlicher Frequenz und Amplitude gebildet werden können. Die Zerlegung einer beliebig geformten, periodischen Zeitfunktion in diese Sinusschwingungen verdanken wir dem französischen Mathematiker Jean-Baptiste Fourier (1768–1830). Seine Erkenntnis: „Jede periodische Zeitfunktion lässt sich als eine Reihe von Summanden darstellen, die jeweils die harmonische Frequenz und Amplitude einer Sinus- und einer Kosinusschwingung repräsentieren.“ Es gilt also:

Man sieht, dass die Frequenz jeder Schwingung mit k > 0 ein Vielfaches der Grundfrequenz ω0 = 2 πf0 ist. Die Fourierkoeffizienten ak und bk erhält man, indem man x(t) mit sin(kω0t) bzw. cos(kω0t) multipliziert und über eine Periode integriert:

Für k = 0 ergibt sich a0 als Gleichanteil von x(t). Wir wollen uns das Resultat einer Fourieranalyse einmal am Beispiel einer Sägezahn- und einer Rechteckfolge verdeutlichen. Die Fourierreihe eines Sägezahnsignals lautet:

die einer Rechteckfolge:

Die Approximation wird umso genauer, je mehr Reihenglieder wir berücksichtigen. Abbildung 5 zeigt oben die Grundschwingung und 8 Oberschwingungen jeder Folge und unten deren Summe. Es fallen besonders beim Rechteck die Überhöhungen an den Flanken auf. Wer glaubt, durch die Berücksichtigung von immer mehr Gliedern der Fourierreihe würde dieser Effekt verschwinden, täuscht sich. Die Höhe des größten „Überschwingers“ liegt bei knapp 18 % der Rechteckhöhe. Weitere Reihenglieder lassen die Überschwinger nur enger zusammenrücken, ändern an ihrer Höhe aber nichts. Dieses so genannte Gibb’sche Phänomen hängt damit zusammen, dass wir an einer Unstetigkeitsstelle (sprungartige Änderung des Rechtecks oder Sägezahns) mit stetigen Funktionen (Sinus und Kosinus) approximieren wollen.

Zwischenergebnis

„Jede periodische Zeitfunktion ist durch die Summation von harmonischen Sinus- und Kosinusschwingungen zu approximieren (Fourieranalyse). Dies gelingt umso besser, je mehr Schwingungen höherer Ordnung man berücksichtigt, hat aber seine Grenzen an Sprungstellen der zu approximierenden Funktion.“ Der Begriff periodisch beinhaltet natürlich die Tatsache, dass die zu approximierende Zeitfunktion schon immer da sein musste und bis in alle Zukunft hinein weiter existiert. In der Praxis haben wir es aber meist mit zeitlich begrenzten, nicht-periodischen Signalen zu tun (eingeschaltet, ausgeschaltet, moduliert …). Die Anwendung der Fourieranalyse führt dann zu mehr oder weniger großen Fehlern. Auf jeden Fall hat jede Zeitfunktion ein korrespondierendes Spektrum und umgekehrt.

Das Oszilloskop

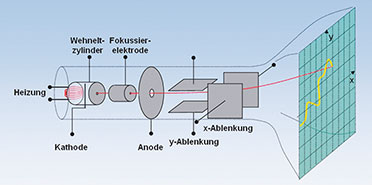
Bild 6: Prinzipieller Aufbau des klassischen analogen Katodenstrahloszilloskops
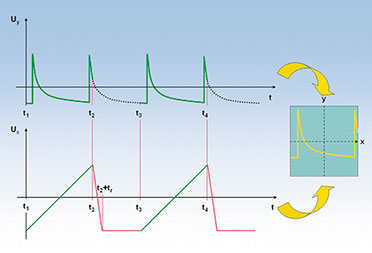
Bild 6: Prinzipieller Aufbau des klassischen analogen Katodenstrahloszilloskops
Der Begriff Oszilloskop leitet sich aus dem Griechischen ab und bedeutet „Schwingungsbeobachter“. In der traditionellen analogen Ausführung wird ein Elektronenstrahl gleichmäßig in waagerechter Richtung (x) über den Leuchtschirm einer Braun ’schen Röhre bewegt und dabei vom Momentanwert der zu messenden Spannung in vertikaler Richtung (y) ausgelenkt. Auf dem Leuchtschirm der Braun’schen Röhre entsteht so ein Abbild des zeitlichen Verlaufs der Messspannung (Abbildung 6). Diese Betriebsart wird auch y-t-Betrieb genannt, weil die x-Richtung mit dem Zeitablauf identisch ist. Die Geschwindigkeit der waagerechten Ablenkung wird von der Frequenz einer Sägezahnschwingung (Zeitbasis) bestimmt, die an den x-Ablenkelektroden anliegt. Der Leuchtschirm ist zum einfacheren Vermessen der angezeigten Signale meist mit einem Raster mit 10 Teilen in x-Richtung und 8 Teilen in y-Richtung überzogen. In y-Richtung wird die Größe des zu messenden Signals in Volts/Div. und in x-Richtung die Zeit in Time/Div. abgelesen. Manche Oszilloskope gestatten es, zwei Zeitsignale gleichzeitig abzubilden. Am einfachsten geht das mit Zweistrahlbildröhren. Aber auch mit einem Schreibstrahl ist das möglich, wenn dieser in zwei aufeinander folgenden horizontalen Strahldurchläufen vom einen Signal und dann vom anderen Signal in y-Richtung abgelenkt wird (Betriebsart „Alternate“). Der Strahl kann aber auch auf seinem Weg über den Schirm kurzzeitig das eine oder das andere Signal repräsentieren, also gewissermaßen zwei zerhackte Kurven erzeugen (Betriebsart „Chop“).
Bild 7: So arbeiten x- und y-Ablenkung mit der Triggerung des Elektronenstrahls zusammen. Sie schneiden stets den gleichen Abschnitt aus dem periodischen Signal aus und erzeugen somit ein stehendes Bild
Bild 7: So arbeiten x- und y-Ablenkung mit der Triggerung des Elektronenstrahls zusammen. Sie schneiden stets den gleichen Abschnitt aus dem periodischen Signal aus und erzeugen somit ein stehendes Bild
Für ein stehendes Bild ist es notwendig, den Lauf des Strahles in horizontaler Richtung bei der gleichen Amplitude des periodischen Signals beginnen zu lassen. Man sagt auch, das Signal triggert (to trigger: auslösen) die x-Ablenkung. Abbildung 7 zeigt die Zusammenhänge. Zum Zeitpunkt t1 bei der auslösenden Spannung Utr startet der in x-Richtung ablenkende Sägezahn bei seinem negativen Minimalwert (Strahl am linken Bildschirmrand), steigt linear auf Null an (Strahl in Bildschirmmitte) und dann weiter auf seinen maximalen positiven Wert (Strahl am rechten Bildschirmrand), den er zu t2 erreicht. Im Zeitintervall t2–t1 hat das Signal den Strahl in y-Richtung ausgelenkt, was die Kurve auf dem Bildschirm erzeugt. Nun wird der Strahl vom Wehneltzylinder dunkel getastet (unterbrochen) und, ohne eine Lichtspur auf dem Bildschirm zu hinterlassen, wieder an den linken Bildschirmrand zurückgeführt (t2+tr). Beim Eintreten der nächsten Triggerbedingung (Utr zu t3) gibt der Wehneltzylinder den Strahl wieder frei, und der nächste Durchlauf startet. So ergibt sich durch das Zusammenwirken von Ux und Uy ein stehendes Bild auf dem Schirm.
Bild 8: Ein täuschend echt arbeitendes virtuelles Oszilloskop, mit dem man sich sehr gut in die Materie einarbeiten kann
Bild 8: Ein täuschend echt arbeitendes virtuelles Oszilloskop, mit dem man sich sehr gut in die Materie einarbeiten kann
Je nach Größe der Ablenkdauer (t2–t1) wird ein mehr oder weniger großer Abschnitt des Zeitsignals abgebildet, was einer horizontalen Stauchung (weniger Bilder pro Sekunde) bzw. einer Dehnung (mehr Bilder pro Sekunde) entspricht. Für eine wohl defi- nierte Laufzeit des Strahls in x-Richtung ist die Zeitbasis des Oszilloskops zuständig. Wie bereits gesagt, setzt das wiederholte Triggern ein periodisches Signal voraus. Für einmalige Zeitvorgänge (one shot) verwendete man früher analoge Speicheroszilloskope, deren Bildröhren das Bild eine bestimmte Zeit lang einfrieren konnten. Im Zeitalter der Digitaltechnik steht das One-Shot-Signal im Speicher des Digitaloszilloskops zur Analyse und Anzeige zur Verfügung. Wer sich mit dem Oszilloskop vertraut machen will, findet auf der Internetseite www.virtuelles-oszilloskop.de von Peter Debik eine schöne Möglichkeit dafür. Hier kann er an einem virtuellen Zweikanaloszilloskop HM 203 der Firma Hameg alle Feinheiten der Bedienung bequem und hintergründig ausloten (Abbildung 8).

Analog oder digital?

Die Verarbeitung eines analogen Messsignals kann analog oder digital erfolgen. Entsprechend spricht man von Analog- oder Digitaloszilloskopen. Beim Digitaloszilloskop findet man die ganze Bandbreite der Methoden zur digitalen Signalverarbeitung: Bandbegrenzen und Abtasten des Signals, A/D-Wandlung mit einer bestimmten Wortlänge, Algorithmen zur Signalmanipulation und D/A-Wandlung … Ein wesentlicher Vorteil digitaler Oszilloskope liegt darin, dass die abgetasteten Signale abgespeichert und in alle möglichen Richtungen hin untersucht werden können. So ist es nicht verwunderlich, dass hochwertige Digitaloszilloskope quasi nebenbei die Funktion eines Spektrumanalysators mit übernehmen und umgekehrt. Auf jeden Fall sind aber Kenntnisse der digitalen Signalverarbeitung erforderlich, sonst kann man deren spezifische Fehler nicht richtig einschätzen und keine dem Messproblem entsprechenden Einstellungen und Auswertungen vornehmen. Die Übernahme von Messdaten in Computer zur weiteren spezialisierten Aufbereitung ist nur mit Digitaloszilloskopen möglich und erweitert deren Nutzen oft beträchtlich. Nicht zuletzt wird bei Digitaloszilloskopen der Bildschirm zum Einblenden wichtiger Informationen eingesetzt: Periodendauer, Frequenz, Spitzen- oder Effektivwert, Anstiegs- und Abfallzeiten, Zeitpunkt der Messung, Toleranzschemen, u. v. m. Mit der Möglichkeit von farblichen Zuordnungen und der Eingabe über einen berührungsempfindlichen Bildschirm (touch screen) erfährt die Bedienerfreundlichkeit eine neue Größenordnung. Die meisten höherwertigen Digitaloszilloskope können über einen Netzwerkanschluss gesteuert und ausgelesen werden (GPIB und Ethernet). Das ist die Voraussetzung für die Einbindung in automatisierte Messumgebungen. Insbesondere die Analyse von transienten (flüchtigen) Vorgängen im Zeit- und Frequenzbereich ist durch die Digitaltechnik viel einfacher. Der zweite Teil dieses Artikels beschäftigt sich mit den grundlegenden Techniken.

Fachbeitrag online und als PDF-Download herunterladen

Inhalt

Sie erhalten den Artikel in 2 Versionen:

online  als Online-Version

pdf  als PDF (4 Seiten)

Sie erhalten folgende Artikel:
  • Oszilloskop und Spektrum-Analyzer Teil 1/2
    • 1 x Journalbericht
weitere FachbeiträgeForen

Oszilloskop und Spektrum-Analyzer Teil 2/2

ELVjournal 05/2006 | keine Kommentare | Bewertung
| 0,99 EUR
Um die Arbeitsweise eines digitalen Spektrumanalysators richtig zu verstehen, ist ein Ausflug in die Grundlagen der digitalen Signalanalyse notwendig. Es würde den Rahmen dieses Artikels sprengen...
mehr lesen  


Hinterlassen Sie einen Kommentar:
  Name
  E-Mail
KATEGORIEN
LESER IN AKTION
Leser testenLeserwettbewerb
ARCHIV
Verzeichnis der FachbeiträgeArchiv der ELVjournalePlatinenfolien
DAS KÖNNTE SIE AUCH INTERESSIEREN