Hallo, Wolfgang SchererLogout
Kontakt
Newsletter
Karriere
 
Sie befinden sich hier: ELVjournal » Journal-Ausgabe 05/2006 » Oszilloskop und Spektrum-Analyzer Teil 2/2 » So funktionierts » Grundlagen/Tabellen/Übersichten

Oszilloskop und Spektrum-Analyzer Teil 2/2

0,00
Aus ELVjournal 05/2006     0 Kommentare
Oszilloskop und Spektrum-Analyzer Teil 2/2

Inhalt des Fachbeitrags

PDF- / Onlineversion herunterladen

Um die Arbeitsweise eines digitalen Spektrumanalysators richtig zu verstehen, ist ein Ausflug in die Grundlagen der digitalen Signalanalyse notwendig. Es würde den Rahmen dieses Artikels sprengen, wenn wir dabei zu sehr ins Detail gingen. In einer kommenden Folge „Einführung in die digitale Signalverarbeitung“ kann der interessierte Leser eventuelle Lücken schließen.

Der Spektrumanalysator

Die Ermittlung der Frequenzkomponenten eines elektrischen Signals ist die Aufgabe eines Spektrumanalysators. Er analysiert also die spektrale Zusammensetzung des Signals, woraus sich der Name ableitet.

Echtzeitanalysator

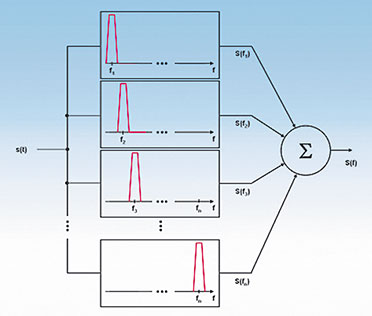
Bild 9: Aus dem Spektrum des Signals werden die einzelnen Frequenzkomponenten herausgefiltert und zur Anzeige gebracht. Nichts anderes macht die Fourieranalyse
Bild 9: Aus dem Spektrum des Signals werden die einzelnen Frequenzkomponenten herausgefiltert und zur Anzeige gebracht. Nichts anderes macht die Fourieranalyse
Eine unmittelbar einleuchtende, aber in der Praxis aus Aufwandsgründen kaum anzutreffende Methode verwendet eine Filterbank. Dabei wird das zu analysierende Frequenzband von Bandfiltern gleichzeitig in Teilbänder zerlegt. Die Frequenzkomponenten des Signals erscheinen nun je nach ihrer Intensität mehr oder weniger stark an den zugeordneten Filterausgängen. Abbildung 9 zeigt schematisch, wie eine Filterbank mit den Mittenfrequenzen f1 bis fn das Zeitsignal s(t) in die Teilspektren S(f1) bis S(fn) zerlegt, die zusammengefasst das Gesamtspektrum S(f) ergeben. Bildet man auf einem Display die Werte S(fμ) für M=1...n über einer f-Achse ab, ergibt sich die grafische Darstellung von S(f). Bei einer feinen spektralen Auflösung ist natürlich eine unwirtschaftlich hohe Anzahl von Filtern mit anspruchsvollen Eigenschaften (exakte Mittenfrequenz, steile Flanken, kurze Einschwingzeiten, zeitliche Stabilität …) erforderlich.

Analoger Spektrumanalysator

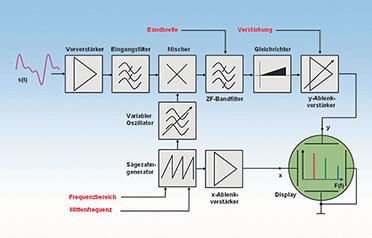
Bild 10: Der analoge Spektrumanalysator hat große Ähnlichkeit mit einem herkömmlichen Radio, das zyklisch über einen bestimmten Empfangsbereich abgestimmt wird
Bild 10: Der analoge Spektrumanalysator hat große Ähnlichkeit mit einem herkömmlichen Radio, das zyklisch über einen bestimmten Empfangsbereich abgestimmt wird
Die Analyse aller interessierenden Frequenzkomponenten durch eine Filterbank lässt sich mit weniger Aufwand realisieren, indem man das zu analysierende Frequenzband an einem festen Filterfenster vorbeischiebt (Abbildung 10). Dazu wird das Eingangssignal mit einer variablen Lokalsoszillatorfrequenz in eine ZF-Lage gemischt, wo ein Bandpassfilter mit fester Mittenfrequenz, aber einstellbarer Bandbreite die jeweiligen Frequenzkomponenten selektiert. Nach deren Gleichrichtung und Verstärkung dienen sie der vertikalen Ablenkung einer Katodenstrahlröhre. Dieser vertikalen Auslenkung des Elektronenstrahls wird eine waagerechte überlagert, die der Frequenz des gefilterten Signals in der Ursprungslage entspricht. Die starre Verkopplung des Lokaloszillators mit der horizontalen Ablenkung ist durch deren Ableitung von einer gemeinsamen Grundfrequenz (im Bild die Frequenz des Sägezahngenerators) sichergestellt.
Bei dieser Art der seriellen Analyse wird also gewissermaßen das Spektrum des Eingangssignals am Analysefilter „vorbei geschoben“. Dabei darf die Geschwindigkeit der Frequenzänderung (sweep time, Wobbelgeschwindigkeit) nicht zu groß sein, damit das Analysefilter genügend Zeit zum Einschwingen hat. Seine Einschwingzeit hängt von der gewählten Bandbreite ab – je schmalbandiger, umso langsamer der Einschwingvorgang. Darin drückt sich das Zeit- Bandbreite-Gesetz der Nachrichtentechnik aus. Bei hoher spektraler Auflösung (schmale Bandbreite) muss der Sweep- Zyklus deshalb so langsam erfolgen, dass sich kein stehendes Bild mehr auf dem Schirm der Katodenstrahlröhre ergibt. Für diesen Fall gibt es Röhren mit Speicherdisplay oder langer Nachleuchtdauer. Die Zwischenfrequenz wird meist oberhalb des Arbeitsbereichs des Spektrumanalysators gewählt, um mit einem einfachen Eingangstiefpass Spiegelfrequenzen zu unterdrücken. Nehmen wir zum Beispiel einen Spektrumanalysator mit einem Arbeitsbereich von wenigen kHz bis 100 MHz mit einer Zwischenfrequenz von 150 MHz an. Der Lokaloszillator muss dann zwischen 150 und 250 MHz abstimmbar sein. Das Spiegelband (fEingang+ 2 fZF) von 300 bis 400 MHz kann also von einem Tiefpass, der keine scharfen Anforderungen erfüllen muss, unterdrückt werden.

Digitaler Spektrumanalysator

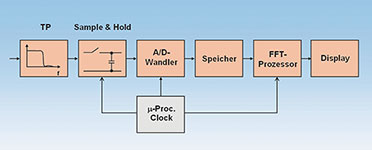
Bild 11: Der digitale Spektrumanalysator digitalisiert das Eingangssignal zunächst und füllt mit den digitalen Signalwerten einen Speicher. Alle weiteren Verarbeitungsschritte beruhen auf diesem Speicherabbild des digitalisierten Signalabschnitts
Bild 11: Der digitale Spektrumanalysator digitalisiert das Eingangssignal zunächst und füllt mit den digitalen Signalwerten einen Speicher. Alle weiteren Verarbeitungsschritte beruhen auf diesem Speicherabbild des digitalisierten Signalabschnitts
Für die digitale Verarbeitung des Eingangsspektrums muss man es bandbegrenzen, einer A/D-Wandlung unterziehen, einen geeigneten Abschnitt (time record) speichern und den Speicherinhalt digital aufbereiten (Abbildung 11). Man entnimmt dem Signal also Proben (Abtasten und Halten, engl. Sample und Hold), wandelt diese in binäre Zahlenwerte einer bestimmten Wortlänge, speichert sie und unterwirft den Speicherinhalt (time record) einer diskreten Fouriertransformation (DFT), bzw. seiner schnellen Variante, der Fast Fourier Transformation (FFT, dafür muss die Anzahl der Abtastwerte eine Zweierpotenz sein: 29=512, 210=1024, 211=2048 …). Die Darstellung der resultierenden Spektren und vieler weiterer Signal- und Verarbeitungsparameter wird heute meist von Flüssigkristalldisplays übernommen.

Abtasttheorem

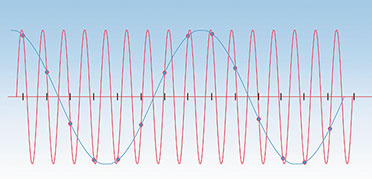
Bild 12: Die blaue Kurve wird unter Einhaltung des Abtasttheorems abgetastet, d. h., es werden ihr mehr als zwei Proben pro Periode entnommen. Anders dagegen die höherfrequente rote Kurve. Beide Abtastungen liefern das gleiche Signal – eine Folge des Alias-Effekts
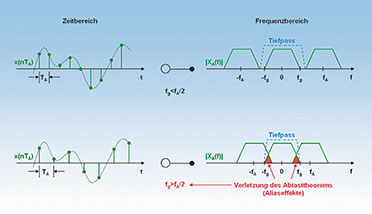
Bild 12: Die blaue Kurve wird unter Einhaltung des Abtasttheorems abgetastet, d. h., es werden ihr mehr als zwei Proben pro Periode entnommen. Anders dagegen die höherfrequente rote Kurve. Beide Abtastungen liefern das gleiche Signal – eine Folge des Alias-Effekts
Der erwähnte bandbegrenzende Tiefpass am Eingang stellt die Einhaltung des Abtasttheorems sicher. Es besagt, dass der höchsten Frequenzkomponente im abzutastenden Signal mindestens zwei Werte pro Periode zu entnehmen sind, um den so genannten Alias-Effekt zu vermeiden und die betreffende Frequenzkomponente wieder restaurieren zu können (Abbildung 12).
Bild 13: Oben: Überabgetastetes Spektrum (links) und das zugehörige Spekt rum (rechts). Unten: Unterabtastung führt zur Überlappung der periodischen Abtastspektren. Durch den Alias-Effekt lässt sich das Ausgangssignal nicht mehr fehlerfrei rekonstruieren
Bild 13: Oben: Überabgetastetes Spektrum (links) und das zugehörige Spekt rum (rechts). Unten: Unterabtastung führt zur Überlappung der periodischen Abtastspektren. Durch den Alias-Effekt lässt sich das Ausgangssignal nicht mehr fehlerfrei rekonstruieren
Bei der Abtastung ergeben sich nämlich bei Vielfachen der Abtastfrequenz periodisch wiederkehrende Spektren, die sich bei Verletzung des Abtasttheorems überlappen würden. Das Basisbandspekt - rum enthielte dann Anteile aus dem ersten Nachbarspektrum und wäre auch nach dem Ausfiltern durch einen Tiefpass irreversibel verfälscht (Abbildung 13).

Diskrete Fouriertransformation

Wir hatten einen Punkt bisher nur etwas beiläufig erwähnt, der aber von großer Wichtigkeit für das Verständnis der Funktionsweise eines Spektrumanalysators ist. Die Fourieranalyse setzt periodische Signale voraus, d. h. Signale, die schon immer eingeschaltet waren und bis in alle Ewigkeit sein werden und deren zeitlicher Verlauf von regelmäßig wiederkehrenden Abschnitten gekennzeichnet ist. Solche Signale sind natürlich nur in der Theorie möglich. In der Praxis sind Signale schon deshalb nicht streng periodisch, weil sie nur eine bestimmte endliche Zeit lang existieren. Aber auch sie haben eine spektrale Darstellung, die wir über die zeitdiskrete Version des Fourierintegrals gewinnen können. An dieser Stelle soll nur kurz, ohne in die Tiefe zu gehen, der Zusammenhang zwischen einer endlichen Folge von Abtastwerten im Zeitbereich und den zugehörigen Spektralwerten im Frequenzbereich abgeleitet werden. Nehmen wir an, es läge ein kontinuierliches Zeitsignal x(t) vor. Dann ist seine Fouriertransformierte die zugehörige Darstellung im Frequenzbereich:

Es sei darauf hingewiesen, dass sowohl x(t) als auch X(ω) komplex sein können.

Von der Abtastfolge zum diskreten Spektrum

Das Abtasten von x(t) entspricht einer Diskretisierung der Zeit, d. h. nur die Signalwerte zu gewissen Zeitpunkten, den Abtastzeitpunkten nTA (im Weiteren wird aus Gründen der Schreibvereinfachung der Index A weggelassen), werden in die weitere Betrachtung einbezogen:


Setzt man dies in das Fourierintegral ein, reduziert sich die Integration auf die Summation der zu den Abtastzeitpunkten herrschenden Werte des Integranden, also wird aus dem komplexen Fourierintegral das komplexe Abtastspektrum der diskreten Fouriertransformation (DFT):

Dies ist das Abtastspektrum einer „immerwährenden“ Zeitfunktion (-∞

Beschränken der Abtastwerte

In der Praxis muss aus Aufwands- und Zeitgründen eine begrenzte Anzahl von Abtastwerten aus der unendlich langen Folge zur Berechnung genügen – gewissermaßen ein endlicher Abschnitt daraus. Wer möchte schon gerne unendlich lange auf sein Messergebnis warten? Jede Zeitaufnahme ist als Ausschnitt zu verstehen, der durch Multiplikation der unendlich langen periodischen Ursprungsfolge mit einer gleich langen Rechteckfunktion (uniform window) gewonnen wird. Bei der Beschränkung der Zahl der Messwerte kann es zu gravierenden Fehlern kommen, die man durch „Fenstern“ (d. h. Multiplizieren der gespeicherten Abtastwerte mit einer Gewichtsfunktion) der Zeitaufnahme zu mildern versucht. Das Fenster ist meist so breit wie der gespeicherte Signalabschnitt. In der Regel ist es zur Mitte des gespeicherten Signalabschnitts symmetrisch und hat dort den Wert 1. Zu den Rändern fällt es mit unterschiedlichem Verlauf auf null ab.

Der Leakage-Effect

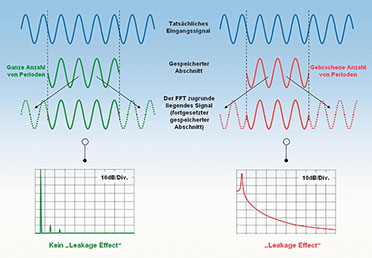
Bild 14: Wenn die periodische Fortsetzung des gespeicherten Signalabschnitts zum periodischen Ursprungssignal führt, tritt kein Leakage-Effect auf (links)
Bild 14: Wenn die periodische Fortsetzung des gespeicherten Signalabschnitts zum periodischen Ursprungssignal führt, tritt kein Leakage-Effect auf (links)
Wie bereits gesagt, setzt die Fouriertransformation voraus, dass ein für alle Zeit wiederholtes Signal vorliegt. In dem in Abbildung 14 links gezeigten Fall führt die Bearbeitung des gewählten Abschnittes einer Sinusschwingung mit zwei kleinen Harmonischen zu keinen Transformationsfehlern, weil im Speicher eine ganze Anzahl von Sinusschwingungen vorliegt. Deren periodische Fortsetzung führt zu einer mit dem tatsächlichen Eingangssignal identischen Sinusschwingung, die der Fouriertransformation zugrunde liegt. Dagegen führt die Zeitaufnahme in Abbildung 14 rechts zu Phasensprüngen im wiederholten Zeitsignal. Damit weicht dieses erheblich vom tatsächlichen Eingangssignal ab. Es verwundert deshalb nicht, dass dies auch Auswirkungen auf die Frequenzdarstellung hat. Wir erhalten ein „verschmiertes“ Abbild des Spektrums (welches sogar die Harmonischen überdeckt) der sauber durchlaufenden Sinusschwingung (leakage effect). Es lässt sich natürlich in der Praxis nicht immer garantieren, ob eine ganzzahlige Anzahl von Schwingungen den Speicher belegt. Damit hängt der Leakage-Effect von Zufälligkeiten ab und das Messergebnis ist nicht verlässlich. Hier setzt das „Fenstern“ an.

Fenstern

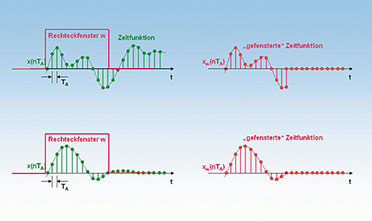
Bild 15: Mit einer Fensterfunktion (hier ein Rechteck: uniform windowing) wird das abgetastete Signal auf eine bestimmte Anzahl von Werten reduziert. Das hat bei ungünstiger Wahl des Ausschnitts Verfälschungen des Signalspektrums zur Folge: Das Spektrum verbreitert sich (leakage effect)
Bild 15: Mit einer Fensterfunktion (hier ein Rechteck: uniform windowing) wird das abgetastete Signal auf eine bestimmte Anzahl von Werten reduziert. Das hat bei ungünstiger Wahl des Ausschnitts Verfälschungen des Signalspektrums zur Folge: Das Spektrum verbreitert sich (leakage effect)
Mathematisch wird die Fensterung durch Multiplikation des gespeicherten Zeitfunktionsabschnitts (time record) mit einer Fensterfunktion beschrieben (Abbildung 15). Bei dieser „Fensterung“ macht man natürlich einen Fehler, der umso größer ist, je mehr die ursprüngliche Zeitfunktion durch die Fensterung verformt wird. Den Effekt einer Fensterung richtig abschätzen zu können, ist eine wesentliche Voraussetzung für die korrekte Interpretation des Ergebnisses einer digitalen Spektrumanalyse. Durch geeignete Wahl der Fensterform (rechteckig, dreieckig, Hanning, Hamming, Kaiser …) lässt sich der Leakage-Effect verringern.
Bild 16: Wenn die periodische Fortsetzung des gespeicherten Signalabschnitts nicht zum periodischen Ursprungssignal führt, verringert „Fenstern“ den Schmiereffekt
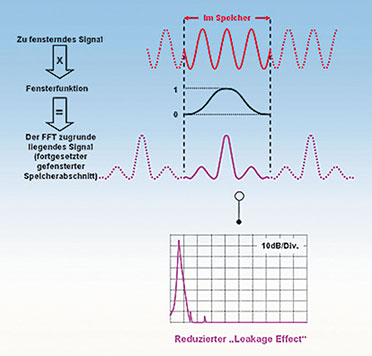
Bild 16: Wenn die periodische Fortsetzung des gespeicherten Signalabschnitts nicht zum periodischen Ursprungssignal führt, verringert „Fenstern“ den Schmiereffekt
Wenn wir in Abbildung 14 rechts den nicht-periodischen Speicherinhalt mit einem sog. Hanning-Fenster bewerten, wird das Spektrum deutlich weniger „verschmiert“ und die stark gedämpften Harmonischen tauchen wieder auf (Abbildung 16). Das liegt daran, dass die Phasensprünge des rechten Signals in Abbildung 14 „wegmultipliziert“ werden. Das Analyseergebnis bezieht sich jetzt allerdings auf eine periodische Folge anund abklingender Bursts, deren Spektrum dem des ursprünglichen Zeitsignals aber schon deutlich näher kommt. Eine schöne, mathematikfreie Einführung in die Grundlagen der Signalanalyse ist die Application Note 243 von Hewlett-Packard, der auch die Abbildungen 14 und 16 entnommen wurden (http://cp.literature.agilent.com/ litweb/pdf/5952-8898E.pdf).

Frequenzauflösung

Mit der Länge des gespeicherten Abschnitts der Zeitfunktion untrennbar verbunden ist die Frequenzauflösung der DFT. Sie entspricht dem Abstand zweier Spektrallinien im Abtastspektrum und beträgt Δf=1/NT (N=Anzahl der Abtastwerte, T=Abtastperiode). Daraus wird deutlich, dass mit wachsenden Ansprüchen an die Frequenzauflösung der DFT die Zahl der gespeicherten Abtastwerte und damit auch die Fensterbreite immer größer werden muss. Für unendlich feine Auflösung (Abstand zwischen zwei Spektrallinien Δf=0) muss der beobachtete Zeitabschnitt und damit die Beobachtungsdauer unendlich lang sein.

Schnelle Fouriertransformation

Angenommen, wir speichern N Abtastwerte aus einer unendlich langen Folge, dann ergeben sich N Spektralwerte gemäß der Formel für die Diskrete Fouriertransformation (DFT):

Dabei ist k die Nummer des Spektralwertes (k=0, …, N-1) und N die Gesamtzahl der Abtast- bzw- Spektralwerte. Die Gleichung bringt zum Ausdruck, dass die Spektralwerte X(k) als komplexe Größe einen Betrag und eine Phase haben. Der Exponentialfaktor wird auch als Drehfaktor WN (engl. twiddle factor) bezeichnet. Unter Ausnutzung seiner Symmetrieund Periodizitätseigenschaften gelangt man zur erheblich schnelleren Fast Fourier Transformation (FFT: Schnelle Fouriertransformation), wobei aber die Anzahl der Abtastwerte eine Potenz von zwei sein muss (N=…, 512, 1024, 2048, …).

Multiplizieren oder Falten

Eine zweite Möglichkeit zur Bestimmung des Spektrums der abgetasteten und gefensterten Zeitfunktion besteht darin, die DFT der ungefensterten Zeitfunktion mit der DFT der Fensterfunktion zu „falten“. Dies beruht auf einem zentralen Gesetz der Nachrichtentechnik, wonach der Multiplikation zweier Zeitfunktionen die Faltung ihrer Spektren entspricht (Multiplikation im Zeitbereich = Faltung im Frequenzbereich). Es würde den Rahmen dieses Artikels sprengen, darauf einzugehen. Mit der Identität

kann man Phase und Betrag des komplexen Spektralwerts leicht berechnen (Pythagoras und arctan). Wer sich etwas hintergründiger für die mathematischen Grundlagen der digitalen Signalverarbeitung interessiert, wird in einer kommenden Serie im „ELVjournal“ bedient.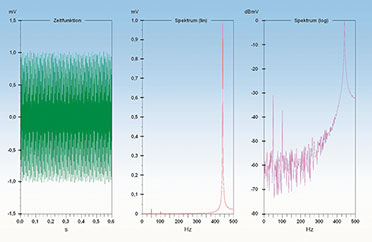
Bild 17: Kann man dem Zeitsignal (links) entnehmen, aus welchen Komponenten es besteht? Wohl kaum. Die Spektren (Mitte und rechts) dagegen sprechen eine klare Sprache
Bild 17: Kann man dem Zeitsignal (links) entnehmen, aus welchen Komponenten es besteht? Wohl kaum. Die Spektren (Mitte und rechts) dagegen sprechen eine klare Sprache
Ein schönes Beispiel für die Nützlichkeit der Fourieranalyse zeigt Abbildung 17. Links ist eine Zeitfunktion dargestellt, wie man sie mit einem Oszilloskop sehen würde (60 ms/Div.). Sie besteht aus einer Grundschwingung von 440 Hz (Kammerton „a“) und zwei Netzbrummstörungen bei 50 Hz und 100 Hz sowie überlagertem Rauschen. Dies ist der Zeitdarstellung beim besten Willen nicht zu entnehmen. Ganz anders dagegen zeigt das Spektrum in der Mitte klar die dominierende 440-Hz-Linie und je eine kleine Linie bei 50 Hz und 100 Hz. Wegen des linearen Maßstabs drohen Letztere fast im Rauschen unterzugehen. Im logarithmisch skalierten Spektrum rechts treten sie deutlich hervor. Durch spezielle Techniken wie Autokorrelation und Mittelwertbildung lassen sich sogar Signale aus dem Rauschen extrahieren, deren Amplitude erheblich kleiner als die der Rauschstörung ist. Die Abbildungen 1, 2, 5 und 17 wurden mit der kostenlosen wissenschaftlichen Software Scilab 4.0, einer interaktiven Programmierumgebung für numerische Anwendungen, berechnet. Scilab ist unter http://www. scilab.org/download/index_download. php?page=release.html aus dem Internet zu beziehen. Dank umfangreicher Dokumentationen mit Anwendungsbeispielen kann man Scilab relativ schnell nutzbringend einsetzen. Mathematische Grundkenntnisse sind allerdings unabdingbar.

Bedienung digitaler Spektrumanalysatoren

Wie beim Oszilloskop ist das Display digitaler Spektrumanalysatoren durch ein Zeilen- und Spaltenraster in rechteckige Teilbereiche unterteilt. In x-Richtung kann man den überstrichenen Frequenzbereich pro Rastereinheit (Frequency Span/Div.) und in y-Richtung die Amplitude (Volts/ Div.) oft auch im logarithmischen Maßstab vorgeben. Ebenso ist die Wahl der gewünschten Fensterfunktion (Window) möglich: Rechteck, Hanning, Hamming, Kaiser … Besonders komfortabel ist die Bedienung von digitalen Spektrumanalysatoren/Oszilloskopen, wenn diese als Steckkarte zum Beispiel für den PCI-Bus eines PCs ausgeführt sind. Dann steht der ganze Bildschirm als virtuelles Bedienpanel zur Verfügung. Dieses kann an das zu lösende Messproblem angepasst werden, Einstellparameter und Messwerte lassen sich abspeichern und später wieder aufrufen (Wiederholbarkeit einer Messung!), die Verwendung der Messwerte in einer weiterverarbeitenden Auswerteund Simulationssoftware ist einfach und die Einbindung in programmgesteuerte Messplätze macht keine Probleme. Auch Varianten für die externen PCSchnittstellen wie den USB (Universal Serial Bus), die parallele Druckerschnittstelle (Centronics) und den Ethernet-Port sind auf dem Markt. So sind auch drahtlose Messungen über WLAN-Netze möglich, was völlig neue Anwendungen ermöglicht.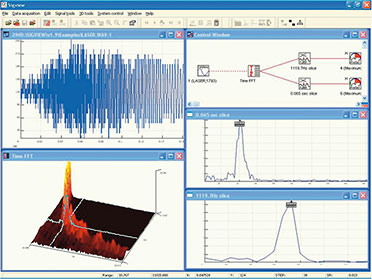
Bild 18: Wenn erst einmal eine genügend große Anzahl von digitalisierten Signalwerten im Speicher ist, kann man daraus (fast) alles berechnen. Mit SigView und einer Soundkarte geht das schon zum Nulltarif. (Quelle: http://www.sigview. com/images/scr6.jpg)
Bild 18: Wenn erst einmal eine genügend große Anzahl von digitalisierten Signalwerten im Speicher ist, kann man daraus (fast) alles berechnen. Mit SigView und einer Soundkarte geht das schon zum Nulltarif. (Quelle: http://www.sigview. com/images/scr6.jpg)
Ein Beispiel für die umfangreichen Auswertungen von abgespeicherten Samples mit Karten verschiedener Hersteller zeigt Abbildung 18 (http://www.sigview.com/ images/scr6.jpg). Der Screenshot basiert auf der Shareware SigView (ca. 100 US-$) der Firma SignalLab. Erste Experimente kann man bereits mit der Soundkarte als Datenaufzeichnungsund Ausgabemedium durchführen und später auf eine anspruchsvolle Mehrkanal- PCI-Steckkarte von National Instruments® oder Measurement Computing® umsteigen. Das ist meistens erheblich preiswerter als die Anschaffung eines Stand-alone-Oszilloskops und -Spektrumanalysators. Bei vielen DSP-Karten (DSP: Digital Signal Processing = Digitale Signalverarbeitung) ist im Lieferumfang bereits umfangreiche Software zur Analyse, Synthese und Visualisierung digitaler Daten enthalten. Oft lassen sich damit vollständige „virtuelle“ Messplätze aufbauen.

Fachbeitrag online und als PDF-Download herunterladen

Inhalt

Sie erhalten den Artikel in 2 Versionen:

online  als Online-Version

pdf  als PDF (5 Seiten)

Sie erhalten folgende Artikel:
  • Oszilloskop und Spektrum-Analyzer Teil 2/2
    • 1 x Journalbericht
weitere FachbeiträgeForen

Oszilloskop und Spektrum-Analyzer Teil 1/2

ELVjournal 04/2006 | keine Kommentare | Bewertung
| 0,99 EUR
Jede Münze hat zwei Seiten! Nur wenn die Beschreibung beider Seiten vorliegt, kann man sich ein vollständiges Bild von ihr machen. Niemand wird an dieser Binsenweisheit zweifeln. Aber ist es...
mehr lesen  


Hinterlassen Sie einen Kommentar:
  Name
  E-Mail
KATEGORIEN
LESER IN AKTION
Leser testenLeserwettbewerb
ARCHIV
Verzeichnis der FachbeiträgeArchiv der ELVjournalePlatinenfolien
DAS KÖNNTE SIE AUCH INTERESSIEREN