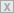Einführung in die digitale Signalverarbeitung Teil 1/8
Aus ELVjournal
02/2007
0 Kommentare
Allgemeines
Für
die klassische Physik und Elektrotechnik sowie die von uns durch unsere
Sinnesorgane erlebte Umwelt bewahrheitet sich das Stetigkeitsaxiom
immer wieder: Temperaturen, Drücke, Wasserstände, Ladungen, Spannungen,
Ströme ... – allgemein formuliert „Signale“ – verändern sich in
endlichen Zeitabschnitten endlich. Diese Eigenart ihres Verhaltens macht
es möglich, den zeitlichen Verlauf durch eine genügend dichte Folge von
Einzelwerten zu beschreiben und die Zwischenwerte durch Interpolation
zu gewinnen. Man erhält die Folgewerte durch regelmäßige Messung des
Signals, was auch als „Abtasten“ bezeichnet wird. Der zeitliche Abstand
der Folgewerte darf nur nicht so groß werden, dass relevante
Signaländerungen zwischen zwei Folgewerten liegen und somit nicht
erkannt werden können. Hier gilt das Prinzip „so selten wie möglich, so
häufig wie nötig“.
Am Beispiel von Messungen des Wasserstandes (Pegel) von Gewässern
wollen wir das verdeutlichen. Diese im Sekundenabstand vorzunehmen,
ist unsinnig, weil sich der Pegel in dieser kurzen Zeit nur unwesentlich
ändert und riesige Messwertetabellen entstünden. Andererseits sind
wöchentliche Messungen zu wenig, da zwischen ihnen die Überschwemmung
ihren Lauf genommen haben könnte. Wir brauchen also eine an die
Veränderungsgeschwindigkeit der Messgröße angepasste Messrate: Schnell
veränderliche Größen müssen häufig gemessen werden, trägere weniger
häufig, damit aus der Folge der Messwerte ein verlässliches Bild vom
Verlauf der Messgröße zu gewinnen ist. Genau diese Erkenntnis schlägt
sich im später erklärten Abtasttheorem der Nachrichtentechnik nieder.Das
elementarste Analog-Signal ist eine sinusförmige Funktion der Zeit.
Deren Amplitude s(t) hängt mit der Frequenz f, der Zeit t, dem
Phasenwinkel φ und der Spitzenamplitude (s^) wie folgt zusammen:
Mit der Definition der Kreisfrequenz Gleichung 3 entspricht dem in Abbildung 1 dargestellten Kurvenverlauf. 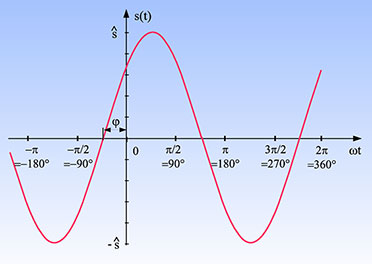
|
| Bild
1: Die grafische Darstellung des zeitlichen Verlaufs einer um den
Phasenwinkel φ voreilenden Sinusschwingung mit der Kreisfrequenz ω und
der Amplitude s^ |
Wir
merken uns an dieser Stelle, dass ein positiver Phasenwinkel die Kurve
nach links zu früheren Zeiten verschiebt. Man sagt auch, die Kurve mit
dem positiven Phasenwinkel im Argument eilt der ohne Phasenwinkel voraus
(voreilend). Das ist leicht verständlich, wenn wir uns einen bestimmten
Punkt der Kurve anschauen, z. B. den Nullpunkt vor der positiven
Halbwelle. Hier ist wegen sin(0)=0 das Argument ωt + φ = 0, woraus ωt =
-φ folgt. Negative Phasenwinkel verschieben die Kurve entsprechend nach
rechts, d. h. zu späteren Zeitpunkten hin (nacheilend).
Die Frequenz f beschreibt, wie viele Schwingungen in einer Sekunde
stattfinden. Ihre Dimension ist demnach 1/s oder Hz (Hertz). Die Dauer
für eine ganze Schwingung ist der Kehrwert ihrer Frequenz und wird als
Periodendauer T mit der Einheit s bezeichnet. Gleichung 4 beschreibt den
Zusammenhang zwischen Periodendauer und Frequenz, Gleichung 5 zwischen
Periodendauer und Kreisfrequenz: Aus
rechnerischen Gründen ist die komplexe Darstellung des Sinus oder
Kosinus oft sehr vorteilhaft. Dazu verwendet man die Eulersche
Identität: Ersetzt man x durch -x folgt: i wird als imaginäre Einheit bezeichnet. Sie ist definiert als Quadratwurzel aus -1. Dementsprechend gilt: Man
kann die Gleichungen 6 und 7 auch grafisch als Einheitszeiger mit der
Länge 1 in der komplexen Ebene darstellen. Abbildung 2 ist die grafische
Entsprechung von Gleichung 6. 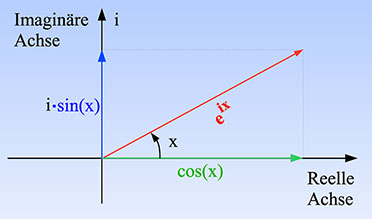
|
| Bild 2: Die Eulersche Identität als Einheitszeiger in der komplexen Ebene |
Wegen
des vertauschten Vorzeichens des Imaginärteils des zu (6) gehörigen
Zeigers erscheint der mit Gleichung 7 korrespondierende Zeiger in
Abbildung 3 an der reellen Achse gespiegelt. 
|
| Bild 3: Die Darstellung aus Bild 2 mit umgekehrtem Vorzeichen des Exponenten |
Auf s(t) angewandt, folgt: Man sieht, dass die reelle Zeitfunktion s(t) gleich dem Imaginärteil des komplexen Ausdrucks ist.
Mit konjugiert komplexen Exponentialausdrücken (Exponenten mit umgekehrten Vorzeichen) kann man s(t) auch wie folgt schreiben: Hat s(t) einen kosinusförmigen Verlauf, gilt: Zeigerdarstellung
An
dieser Stelle sollte man sich die Darstellung einer phasenverschobenen
Sinus- bzw. Kosinusschwingung mit der Spitzenamplitude 1 durch zwei in
der komplexen Ebene gegenläufig mit der Frequenz ω rotierende Zeiger mit
der halben Länge der Spitzenamplitude grafisch verdeutlichen. Abbildung
4 zeigt dies für die Sinusschwingung.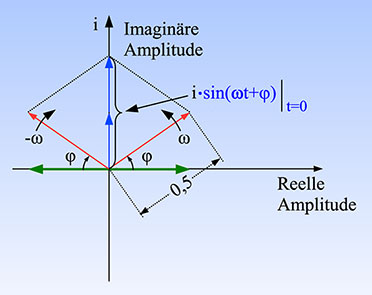
|
| Bild 4: Die Sinusschwingung als Projektion zweier gegenläufiger, zur imaginären Achse symmetrischer Zeiger |
Zum
Zeitpunkt t = 0 ist die Lage der beiden Zeiger der Länge 0,5 nur durch
den Phasenwinkel φ bestimmt. Wir erkennen, dass sich die Projektionen
auf die reelle Achse (cos) aufheben und die auf die imaginäre Achse
(sin) addieren. Weil die rotierenden Zeiger die Länge 0,5 haben,
entspricht die Summenlänge ihrer Projektionen (vektorielle Addition) auf
die imaginäre Achse der Projektion eines einzelnen Zeigers der Länge 1.
Die Kosinusschwingung illustriert Abbildung 5, ebenfalls zu t = 0.
Hier heben sich die Projektionen auf die imaginäre Achse (sin) auf und
jene auf die reelle Achse (cos) addieren sich. 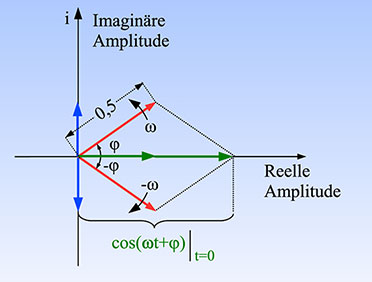
|
| Bild 5: Die Kosinusschwingung als Projektion zweier gegenläufiger, zur reellen Achse symmetrischer Zeiger |
Das
Gesagte gilt natürlich auch für jeden beliebigen Zeitpunkt t >0, wo
dann das Argument der e-Funktion bzw. des Sinus/Kosinus entsprechend
größer ist. Ein voller Umlauf der Zeiger um 2ϖ (das Bogenmaß 2ϖ
entspricht 360° im Winkelmaß) beschreibt eine Periode der Schwingung.
Die Kurve hat nach t = 2ϖ/ω = Τ eine Periode durchlaufen und den
gleichen Wert wie nach t = nΤ für alle ganzzahligen Werte von n. Man
sagt, auch der Sinus sowie der Kosinus sind periodisch in 2ϖ.
Eine allgemeingültige Formulierung für eine in T periodische
Zeitfunktion lautet: Gerade und ungerade Funktionen
Es
ist für die Rechenpraxis ungemein praktisch, die Symmetrieeigenschaften
von Funktionen zu kennen. Wenn eine Funktion spiegelsymmetrisch zur
Ordinatenachse ist, spricht man von einer geraden Funktion. In der
Formelsprache ausgedrückt, ist eine Funktion gerade, wenn gilt:Ungerade Funktionen sind punktsymmetrisch zum Ursprung. Für sie gilt: Abbildung 6 demonstriert die Symmetrieeigenschaften. 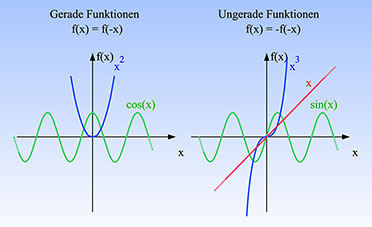
|
| Bild 6: Gerade Funktionen sind spiegelsymmetrisch zur Ordinate (y-Achse), ungerade punktsymmetrisch zum Ursprung der xy-Ebene. |
Harmonische Analyse periodischer Signale
Periodische
Signale bestehen aus gleichen Abschnitten, die sich alle T Sekunden
wiederholen und dies von jeher bis in alle Ewigkeit. Diese ewig währende
Periodizität ist natürlich bei realen Signalen nie gegeben, da diese
irgendwann einmal eingeschaltet und auch wieder ausgeschaltet werden.
Aber je mehr Periodenlängen aneinander gereiht sind, umso mehr nähert
man sich dem Idealzustand mit einer unendlichen Zahl von Perioden.
Jedes periodische Signal lässt sich als unendliche Summe gewichteter
sinusförmiger Schwingungen darstellen. Im „ELVjournal“ 4/06 wurde in dem
Artikel „Oszilloskop und Spektrum-Analyzer“ die Zerlegung eines
periodischen Signals in seine Harmonischen beschrieben. Im Gegensatz zu
der dort verwendeten Darstellung benutzen wir hier die komplexe
Notation:Die im Allgemeinen komplexen Fourierkoeffizienten Fn berechnet man über:
Die
Integration muss über eine Periode des Signals erfolgen, wobei t0 als
untere Integrationsgrenze beliebig gewählt werden kann, am besten so,
dass sich die Rechnung möglichst einfach gestaltet. Wir wollen an dieser
Stelle festhalten, dass jedes periodische Signal aus einer
Grundschwingung und unendlich vielen Harmonischen (Oberschwingungen mit
Frequenzen, die Vielfache der Frequenz der Grundschwingung sind)
besteht. Harmonische Analyse nicht-periodischer Signale
Auch
Signale, die nicht periodisch sind (diese nennt man auch aperiodisch),
kann man aus Sinuskomponenten bilden. Dazu dienen die Fourierintegrale:F(iω)
ist das komplexe Spektrum (oder genauer formuliert: die spektrale
Dichtefunktion) der aperiodischen Zeitfunktion f(t). Häufig ist die
folgende symbolische Schreibweise für den Fourierintegralzusammenhang
von Zeitfunktion und Spektrum anzutreffen: Die
Auswertung der Integrale (18) und (19) zur Ermittlung des
Frequenzspektrums einer Zeitfunktion bzw. umgekehrt kann schwierig sein.
Deshalb benutzt man in der Praxis Korrespondenztabellen, in denen die
meisten Transformationen bereits zusammengestellt sind.
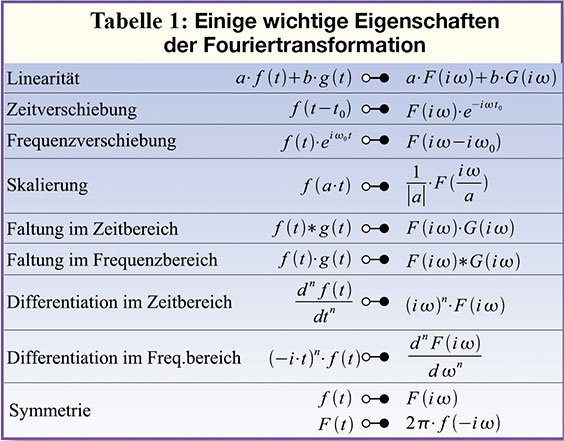
Unter Berücksichtigung der wichtigsten Eigenschaften der
Fouriertransformation (Tabelle 1) kann man auf diese Weise viele
Fourierintegrale durch Analogieüberlegungen „lösen“. Im
nächsten Teil dieser Serie werden die Fourierkorrespondenzen wichtiger
Funktionen und die wichtigsten allgemeinen Eigenschaften der
Fouriertransformation besprochen. Fachbeitrag als PDF-Download herunterladen
Inhalt
Sie erhalten den Artikel in 1 Version:
 als PDF (3 Seiten)
als PDF (3 Seiten)
Sie erhalten folgende Artikel:
- Einführung in die digitale Signalverarbeitung Teil 1/8
| weitere Fachbeiträge | Foren | |
Hinterlassen Sie einen Kommentar:






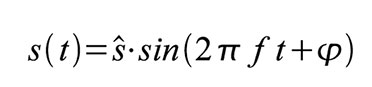
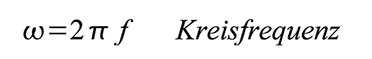
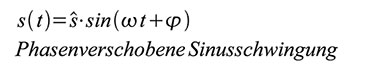


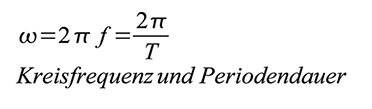
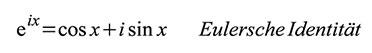
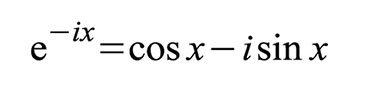
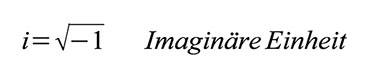
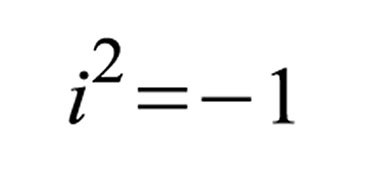


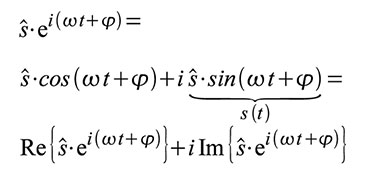
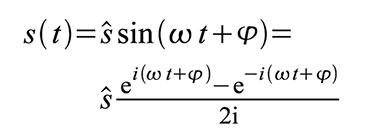
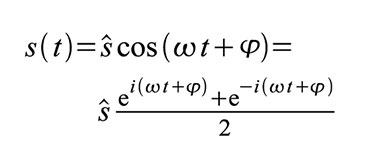


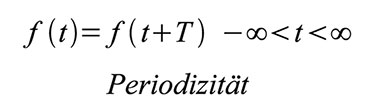
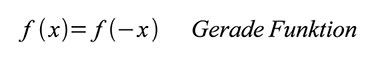
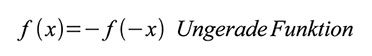



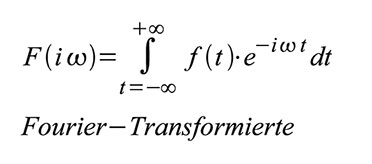
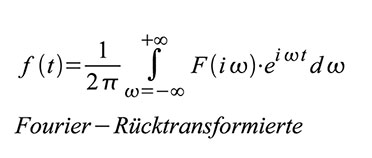
 als PDF (3 Seiten)
als PDF (3 Seiten)