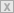Einführung in die digitale Signalverarbeitung Teil 2/8
Aus ELVjournal
03/2007
0 Kommentare
Fourierkorrespondenzen
|
| Bild 7: Drei elementare Fourierkorrespondenzen. Von oben: Dirac-Impuls, Sinusschwingung und Kosinusschwingung. |
Eine
solche unendlich schmale und unendlich hohe „klassische Funktion“ gibt
es nicht. Der δ-Impuls ist nur als so genannte Distribution mathematisch
sauber definierbar. Distributionen sind „verallgemeinerte Funktionen“,
die vom französischen Mathematiker Laurent Schwartz (1915–2002) in der
Mitte des vorigen Jahrhunderts theoretisch untermauert wurden
(Distributionentheorie). Als Hilfsmittel finden Distributionen
vielfältige Anwendungen, z. B. in der Theorie der gewöhnlichen und
partiellen Differentialgleichungen, der Fourier-Analysis, der Physik
oder der Elektrotechnik. Der δ-Impuls ist als Distribution über seine
Ausblendeigenschaft gemäß Gleichung (22) definiert. Obwohl der δ-Impuls
keine klassische Funktion ist, lässt er sich dennoch auch ohne tiefere
Kenntnisse der Theorie der Distributionen äußerst fruchtbar in der
Systemtheorie einsetzen. 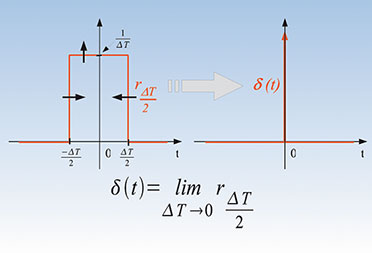
|
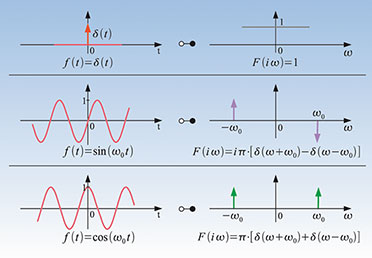
| Bild 8: Der Dirac- Impuls als Grenzübergang eines Rechteckimpulses mit der Fläche 1 (Breite ΔT x Höhe 1/ΔT) für ΔT → null |
Das
Spektrum des δ-Impulses hat bei allen Frequenzen die Amplitude 1. Man
kann sich das auch veranschaulichen, indem man die Fouriertransformierte
eines Rechteckimpulses der Breite ΔT und der Höhe 1/ΔT betrachtet. Sie
ist eine si-Funktion mit den Nullstellen bei Vielfachen von 1/ΔT und
einer Amplitude der Hauptkeule von 1. Je schmaler das Rechteck wird,
umso weiter wandern die Nulldurchgänge vom Ursprung der Frequenzachse
weg. Im Grenzübergang wird die si-Funktion zu einer Parallelen im
Abstand 1 zur ω-Achse gespreizt. Mit anderen Worten: Ein unendlich
kurzes Ereignis im Zeitbereich hat ein konstantes Spektrum im
Frequenzbereich zur Folge. Allgemeiner formuliert: Je kürzer das
Zeitereignis, umso breiter seine Entsprechung im Frequenzbereich. Dies
ist nichts anderes als das Zeit-Bandbreite- Gesetz der
Nachrichtentechnik. Etwas Vergleichbares können wir bei einem
Schwingkreis beobachten. Ist er schmalbandig (verlustarm), wirkt eine
Anregung als langsam abklingende Schwingung nach. Der breitbandige
(verlustreiche) Schwingkreis schwingt dagegen nur kurz nach. Eine
besonders wichtige Eigenschaft des δ-Impulses für die Beschreibung eines
nachrichtentechnischen Übertragungssystems ist seine
Ausblendeigenschaft. Die Erklärung: Weil δ(t-τ) nur für das Argument τ = t ungleich null ist, lässt sich das Integral auch schreiben als: Das
Integral über den δ-Impuls ist definitionsgemäß 1, was (23) zur
Identität macht und so die Gültigkeit von (22) bestätigt. Die zweite
Fourierkorrespondenz in Abbildung 7 betrifft die periodische
Zeitfunktion einer immerwährenden Sinusschwingung (sozusagen die Mutter
aller periodischen Funktionen) mit der Frequenz ω0. Ihre
Fouriertransformierte ist rein imaginär (violette Farbdarstellung) und
besteht aus zwei δ-Funktionen, eine mit positivem Vorzeichen bei -ω0 und
eine mit negativem Vorzeichen bei +ω0. Die dritte Fourierkorrespondenz
in Abbildung 7 zeigt das Transformationspaar einer periodischen
Kosinusschwingung mit der Frequenz ω0. Deren Fouriertransformierte ist
rein reell (grüne Farbdarstellung) und besteht ebenfalls aus zwei
δ-Funktionen, beide mit positivem Vorzeichen bei -ω0 und +ω0. Bereits
jetzt erkennen wir zwei wichtige Eigenschaften der
Fouriertransformation: Satz 1: Gerade Zeitfunktionen haben ein reelles,
gerades Spektrum. Satz 2: Ungerade Zeitfunktionen haben ein imäginäres,
ungerades Spektrum. Zeitfunktionen, die weder gerade noch ungerade sind,
haben ein komplexes Spektrum, das natürlich auch weder gerade noch
ungerade ist. Das folgt unmittelbar aus der Tatsache, dass sich jede
Zeitfunktion in eine Summe aus einem geraden und einem ungeraden
Summanden zerlegen lässt, deren Spektren sich nach Satz 1 als reell und
nach Satz 2 als imaginär ergeben. Beide ergänzen sich zu einem komplexen
Spektrum. Das eben Gesagte wird in Abbildung 9 beispielhaft
illustriert. 
|
| Bild
9: Die Fouriertransformierte einer beliebigen, in einen geraden und
einen ungeraden Anteil zerlegbaren Funktion ist wegen der
Linearitätseigenschaft der Fouriertransformation gleich der Summe der
Fouriertransformierten dieser Anteile. Am Beispiel der abklingenden
e-Funktion (oben), ihrem geraden Anteil (Mitte) und ihrem ungeraden
Anteil (unten) kann man sich das verdeutlichen. |
Wir
wollen das mathematisch nachvollziehen. Die obere Zeitfunktion in
Abbildung 9 ist eine abklingende Exponentialfunktion, deren Werte für
negative Zeiten (t<0) durch Multiplikation mit der so genannten
Sprungfunktion u(t) (0 für t<0 und 1 für t>0) auf null gesetzt
werden. Sie hat die rechts in Abbildung 9 für a = 1 abgebildete komplexe Fouriertransformierte: Der
Realteil ist der grüne gerade, der Imaginärteil der violette ungerade
Kurvenzug. Nun kann man die obere Zeitfunktion (24) auch als halbierte
Summe der mittleren und unteren Zeitfunktionen in Abbildung 9
darstellen, deren jeweilige Korrespondenzen rechts stehen. Die Summe
dieser Korrespondenzen muss wegen der Linearitätseigenschaft der
Fouriertransformation (siehe Tabelle 1 im Teil 1) also wieder (25)
ergeben. Wir prüfen das nach: 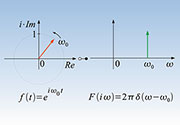
|
| Bild
10: Der mit ω0 rotierende Einheitsdrehzeiger in der komplexen Ebene
(links) hat nur eine Spektrallinie bei ω0 (rechts) als Korrespondenz im
Frequenzbereich. |
Zwei Rechenbeispiele
Wenn
auch nahezu alle denkbaren Transformationspaare Korrespondenztabellen
entnommen werden können, wollen wir doch wenigstens an zwei Beispielen
die Fouriertransformation „von Hand“ demonstrieren.Beispiel 1
Zuerst
betrachten wir die abklingende e-Funktion entsprechend (24) nach der
Definitionsgleichung (18). Noch einige Worte zum Gang der Rechnung in
(27) für alle, die nicht (mehr?) ganz sattelfest beim Integrieren sind.
Der Tatsache, dass es sich um eine bei t = 0 eingeschaltete abklingende
e-Funktion handelt, trägt das Ersetzen der unteren Integralgrenze t = -∞
durch t = 0 Rechnung. Die Stammfunktion für t = ∞ ist null, für t = 0
ist der e-Term gleich 1 und es verbleibt das Ergebnis.Beispiel 2
Nehmen
wir an, wir wollen eine Kosinusschwingung (Abbildung 14) –
eingeschaltet bei t = -Tr/2 und ausgeschaltet bei t = +Tr/2 – aus dem
Zeitbereich in den Frequenzbereich transformieren. Wir setzen die
Kosinusfunktion in das Integral und berücksichtigen die Ein- und
Ausschaltzeitpunkte in den Integralgrenzen (28). Wir verwenden die
Identitäten in (29a) und (29b), setzen Sie in (28) ein und erhalten
(30).Der
Integrand besteht jetzt nur noch aus einer Summe einfacher Sinus- und
Kosinusfunktionen, die summandenweise integriert wird (31). Die geraden
Kosinusfunktionen heben sich nach dem Einsetzen der Integrationsgrenzen
auf und es bleibt die Formel (32). 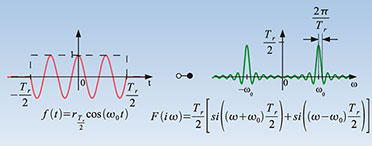
|
| Bild
14: Hier wurde mit einer Rechteckfunktion ein Abschnitt aus einer
Kosinusschwingung erzeugt, sie wurde gewissermaßen ein- und dann
ausgeschaltet. Die Dirac-Impulse, die eine unendlich lange Schwingung im
Frequenzbereich charakterisieren, verändern sich dadurch zu
si-Funktionen. |
Sprungfunktion
|
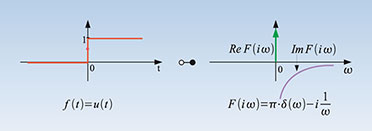
| Bild
11: Die Sprungfunktion ist im Bereich negativer Zeiten null und springt
bei t = 0 auf den Wert 1. Durch Multiplikation mit ihr kann man
periodische Zeitfunktionen „einschalten“. |
Signumfunktion
|
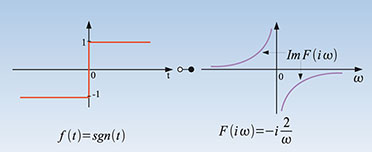
| Bild
12: Die Signumfunktion springt bei t = 0 von -1 auf +1. Die
Multiplikation einer Sinus- oder Kosinusschwingung mit der
Signumfunktion bewirkt an der Sprungstelle deren Phasendrehung um 180°. |
Rechteckfunktion
Von großer Wichtigkeit ist auch die Rechteckfunktion (Abbildung 13). Sie ist definiert als (36).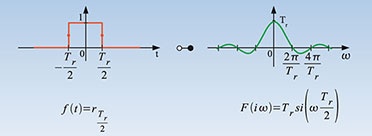
|
| Bild
13: Die Rechteckfunktion kann zum Ausschneiden eines endlichen
Abschnitts aus einer unendlich langen Funktion verwendet werden. Man
spricht dann auch von einem „Rechteckfenster“. |
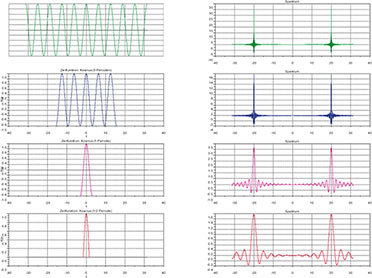
|
| Bild
15: Hier kann man die Wirkung der Fensterbreite studieren. Je schmaler
das Fenster im Zeitbereich, umso mehr „zerlaufen“ im Frequenzbereich die
si-Funktionen. Je breiter das Fenster, desto mehr werden sie gestaucht. |
Dreiecksfunktion
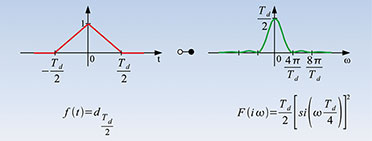
|
| Bild 16: Auch die Dreiecksfunktion kann zum „Fenstern“ verwendet werden. |
Fachbeitrag als PDF-Download herunterladen
Inhalt
Sie erhalten den Artikel in 1 Version:
 als PDF (5 Seiten)
als PDF (5 Seiten)
Sie erhalten folgende Artikel:
- Einführung in die digitale Signalverarbeitung Teil 2/8
| weitere Fachbeiträge | Foren | |
Hinterlassen Sie einen Kommentar:








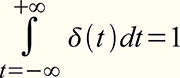
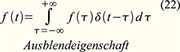
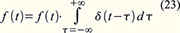

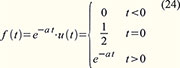
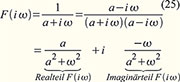
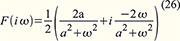

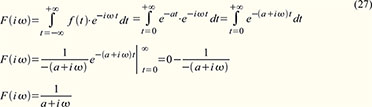

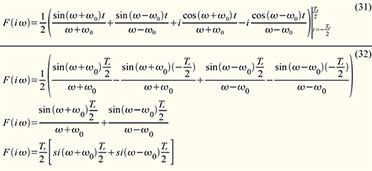








 als PDF (5 Seiten)
als PDF (5 Seiten)