Einführung in die digitale Signalverarbeitung Teil 3/8
Aus ELVjournal
04/2007
0 Kommentare
Das Parseval’sche Theorem
Benannt
nach dem französischen Mathematiker Marc-Antoine Parseval des Chênes
(1755–1836), beschreibt es die Gleichheit der Gesamtenergie eines
reellen Signals im Zeitbereich x(t) und der desselben im Frequenzbereich
X(iω). Parseval erschien die Aussage seines Theorems so offensichtlich
(schließlich handelt es sich hierbei ja nur um zwei verschiedene
Sichtweisen ein und desselben Signals), dass er auf einen Beweis
verzichtete. Die Parseval’sche Formel lautet:Während
die linke Seite von (39) die Zeitintegration der Momentanleistung –
eine Energie – darstellt, beschreibt die rechte Seite das
Frequenzintegral über die Energiedichte – also ebenfalls eine Energie.
Die rechte Seite von (39) leitet sich aus der Fouriertransformierten der
so genannten Autokorrelation eines Energiesignals ab. Das Wort
Korrelation kommt aus dem Lateinischen und bedeutet dort so viel wie
Wechselbeziehung. In der Systemtheorie der Nachrichtentechnik beschreibt
man mit der Kreuzkorrelationsfunktion (KKF) das Maß der Ähnlichkeit
zweier Funktionen: Die Kreuzkorrelierte (KKF) zweier Energie-
Zeit-Funktionen x(t) und y(t) lautet: 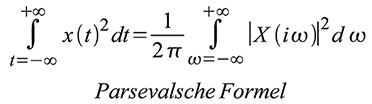
|
| Gleichung 39 – Parseval’sche Formel |
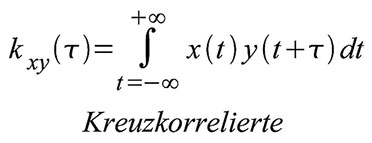
|
| Gleichung 40 – Kreuzkorrelierte |
Mathematisch
gesehen verschiebt man eine der Funktionen um einen gewissen zeitlichen
Abstand τ und integriert das Produkt mit der anderen, unverschobenen
Funktion über die Zeit. Bei Funktionen mit geringen Wechselbeziehungen
ergeben sich kleine Kreuzkorrelierte. Stellt man sich vor, die beiden
Zeitfunktionen würden sich immer ähnlicher (bis zur Gleichheit), geht
die Kreuzkorrelierte in die Autokorrelierte über. Die Autokorrelierte
(AKF) einer Zeitfunktion x(t) lautet also: 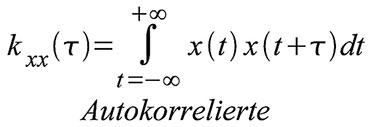
|
| Gleichung 41 – Autokorrelierte |
Auf
den ersten Blick scheint es vielleicht merkwürdig, ein Signal mit
seiner zeitverschobenen Kopie zu multiplizieren und das Produkt zu
integrieren. Aber die ses Verfahren hat sich hervorragend bewährt, um
schwache und stark verrauschte elektromagnetische Signale aufzuspüren.
Zum Beispiel wird in einem Radarsystem das mit Rauschen überlagerte
schwache und laufzeitverschobene Echo x(t + τ) mit dem Sendesignal x(t)
verglichen, indem man die Variable τ so lange verändert, bis die AKF
maximal ist. Dann ist man einerseits sicher, das richtige Signal und
kein Störecho zu empfangen, und kann aus der gefundenen Laufzeit τ den
Abstand zum reflektierenden Objekt berechnen. Bei Funkwellen, die sich
mit Lichtgeschwindigkeit 300.000 km/s ausbreiten, und unter
Berücksichtigung der Tatsache, dass die Laufstrecke des Signals der
doppelten Entfernung zum reflektierenden Objekt entspricht, führt τ =
200 μs zu einem Objektabstand von 30 km. Ein weiteres Beispiel ist die
Mustererkennung in einem Bild, wie sie bei der Überwachung und Steuerung
industrieller Prozesse, des Straßenverkehrs, bei der Bildanalyse usw.
stattfindet. Hier wird statt der eindimensionalen Zeitvariablen (t) aber
mit den zweidimensionalen Ortsfrequenzvariablen (x, y) gearbeitet. Das
führt zu erheblichem Rechenaufwand und schließt eine
Echtzeitverarbeitung oft aus. Über die AKF zur Parseval’schen Formel
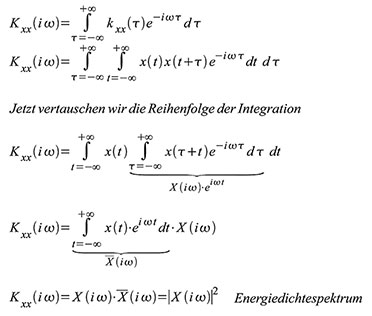
|
| Gleichung 42 |
Es
gibt verschiedene Wege, die Parseval’sche Formel herzuleiten. Einer
davon ist die Anwendung des Faltungssatzes, den wir später noch
ausführlich beleuchten. Ein anderer Weg führt über die AKF. Setzt man
die Autokorrelierte nach (41) in die Definitionsgleichung der
Fouriertransformation (18) ein, ergibt sich (42). Im Gang der Rechnung
haben wir vom Zeitverschiebungssatz aus Tabelle 1 Gebrauch gemacht und
berücksichtigt, dass eine reelle Zeitfunktion ein Spektrum mit geradem
Realteil und ungeradem Imaginärteil hat. Der Zeitverschiebungssatz
begründet die Anschrift: Mit dem Satz über reelle Zeitfunktionen können wir herleiten, dass: Offensichtlich
wäre die linke Seite der Gleichung bei einem negativen Vorzeichen des
Exponenten der e-Funktion definitionsgemäß gleich X(iω). Wegen des
positiven Exponenten erhalten wir aber X(–iω). Weil x(t) reell ist,
gilt: Re[X(–iω)] = Re[X(iω)] und Im[X(–iω)] = –Im[X(iω)], d. h. der
Realteil hat sich nicht verändert, der Imaginärteil dagegen sein
Vorzeichen umgekehrt, was zu zeigen war. Kxx(iω) stellt als
Fouriertransformierte der Autokorrelierten des Zeitsignals x(t) dessen
Energiedichte dar, man nennt Kxx(iω) deshalb auch das
Energiedichtespektrum von x(t). Um zur Parseval’schen Gleichung zu
gelangen, ist es nur noch ein kleiner Schritt. Die Gesamtenergie des
Zeitsignals berechnet sich aus (41) als (43). Um aus der Identität in
der letzten Zeile von (42) wieder die erzeugende Zeitfunktion zu
ermitteln, müssen wir diese als inverse Fouriertransformierte ausdrücken
(44). Gleichung (43) und (44) (mit τ = 0) werden jetzt gleichgesetzt
und es folgt die Parseval’sche Formel, wie in (39) angegeben. 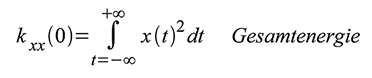
|
| Gleichung 43 – Gesamtenergie |
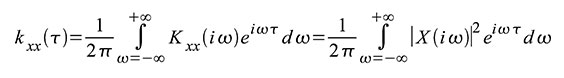
|
| Gleichung 44 |
Ein praktisches Beispiel zum Parseval’schen Theorem
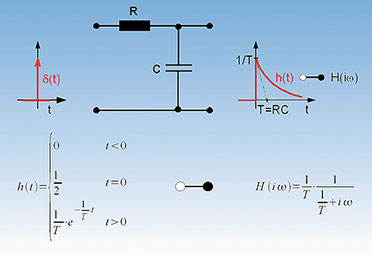
|
| Bild
17: Der RC-Tiefpass ist ein Spannungsteiler, dessen unterer
Teilerwiderstand ein Kondensator ist. Sein Widerstand nimmt mit
zunehmender Frequenz ab und damit auch die Ausgangsspannung des Teilers. |

|
| Gleichung 45 – Signalenergie der Zeitfunktion |
|
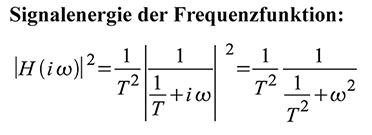
| Gleichung 46 – Signalenergie der Frequenzfunktion |
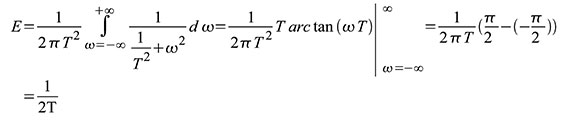
|
| Gleichung 47 |
Funktionsverläufe zeichnen
|
| Bild 18: Mit wenigen Zeilen ist ein kleines Programm geschrieben, das die Funktion sin(x)/x als Grafik ausgibt. |
Vom analogen zum digitalen Signal
Analoge
Signale sind innerhalb ihres Wertebereichs durch eine unendlich feine
Stufung bezüglich Zeit und Amplitude gekennzeichnet. Man sagt auch:
„Analogsignale sind zeit- und wertekontinuierlich“. Entnimmt man ihnen
zu regelmäßigen Zeitpunkten Werteproben – diesen Vorgang bezeichnet man
auch als Abtasten –, haben wir zunächst die Zeit diskretisiert, aber
immer noch einen kontinuierlichen Wertebereich. Typische Vertreter
solcher zeitdiskreten, aber wertekontinuierlichen Systeme sind
SC-Filter, bei denen ohmsche Widerstände durch periodisch umgepolte
Kondensatoren (SC: switched capacitor) ersetzt werden. Bei voll digital
arbeitenden Schaltungen geht man noch einen Schritt weiter und ordnet
den analogen Abtastwerten digitale Zahlenwerte zu. Diese werden durch
Binärwörter mit endlicher Wortlänge repräsentiert, woraus eine gewisse
„Granularität“ der Amplitudendarstellung resultiert. Jetzt haben wir es
also mit einer zeit- und wertediskreten Präsentation des Signals zu tun.Das Abtasttheorem

|
| Bild 19: Claude Elwood Shannon hat die Nachrichtentechnik viel zu verdanken. |
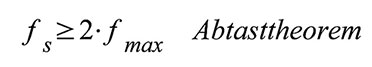
|
| Gleichung 48 – Das Abtasttheorem |
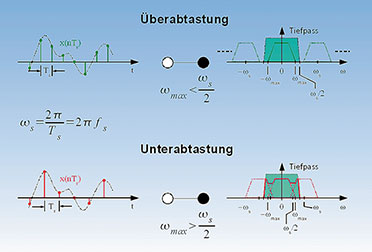
Für
die Einhaltung des Abtasttheorems ist also eine Begrenzung der
Bandbreite des abzutastenden Signals (Bandbegrenzung) erforderlich. Dazu
dient ein analoger Tiefpass, dessen Grenzfrequenz gleich oder kleiner
als die halbe Abtastfrequenz sein muss. Damit ist sichergestellt, dass
keine hohen Frequenzanteile im abzutastenden Signal enthalten sind,
welche das Abtasttheorem verletzen und so genannte Alias-Effekte
hervorrufen würden. In der Praxis ist es wegen der endlichen
Flankensteilheit des analogen Tiefpasses üblich, die Abtastfrequenz
deutlich größer als die doppelte Maximalfrequenz im Signal zu wählen. 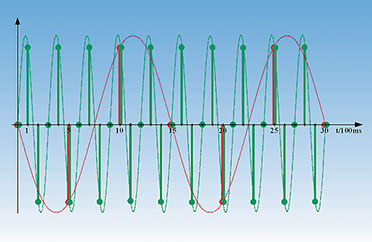
|
| Bild 20: Wird das Abtasttheorem nicht eingehalten, entstehen Aliasfrequenzen |
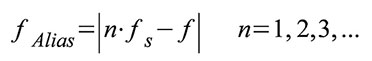
|
| Gleichung 49 |
n
ist als ganze Zahl so zu wählen, dass der Betrag von nfs – f den
kleinstmöglichen Wert annimmt. Im Beispiel von Abbildung 20 wäre demnach
n = 2, woraus die Aliasfrequenz (2 • 2 – 31/3) Hz = 2/3 Hz folgt. Ein
weiteres Beispiel: Vier Frequenzen f1 = 25 Hz, f2 = 70 Hz, f3 = 160 Hz
und f4 = 510 Hz werden mit fs = 100 Hz abgetastet. Bei der Abtastung von
f2, f3 und f4 wird das Abtasttheorem verletzt und es entstehen die
Aliasfrequenzen f2 Alias = Betrag von (100 – 70) Hz = 30 Hz, f3 Alias =
Betrag von (200 – 160) Hz = 40 Hz sowie f4 Alias = Betrag von (500 –
510) Hz = 10 Hz. Die Wirkung einer Unterabtastung ist auch in alten
Westernfilmen in Gestalt sich scheinbar rückwärts drehender Wagenräder
und als Stroboskopeffekt in der Diskothek beobachtbar. Der Abtastvorgang
wird mathematisch durch die Multiplikation einer kontinuierlichen
Zeitfunktion x(t) mit einer regelmäßigen Folge von Dirac-Impulsen ss(t)
beschrieben. Der zeitliche Abstand der Dirac-Impulse entspricht der
Abtastperiode Ts. Durch die Ausblendeigen - schaft des Dirac-Impulses
wird nur der Funktionswert von x(t) selektiert, der zum Zeitpunkt des
Dirac-Impulses existiert. Gleichung (50) drückt dies aus. 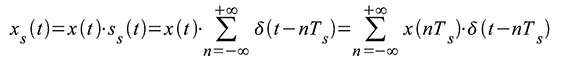
|
| Gleichung 50 |
Um
aus dieser Gleichung weitere Erkenntnisse bequem ableiten zu können,
werden wir uns jetzt ein wenig mit der Faltung – im Englischen
Convolution genannt – beschäftigen. Multiplizieren hier – Falten dort
Aus
Tabelle 1 wissen wir, dass die Multiplikation zweier Zeitfunktionen der
Faltung ihrer Spektren (auf Englisch: convolution) entspricht bzw.
umgekehrt. Doch was ist nun eine Faltung zweier Funktionen? Mathematisch
gesprochen ist die Faltung eine Vorschrift, nach der zwei Funktionen
x1(t) und x2(t) auf eine dritte Funktion y(t) abgebildet werden. Das
hört sich komplizierter an, als es ist. Im analogen Zeitbereich ist die
Faltung zweier Funktionen wie in Gleichung (51) definiert. Im
Frequenzbereich ist die Fouriertransformierte von y(t) gleich dem
Produkt der Fouriertransformierten von x1(t) und x2(t), wie in Gleichung
(52) dargestellt.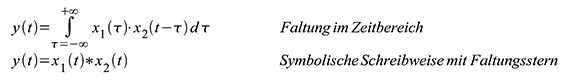
|
| Gleichung 51 – Faltung im Zeitbereich und symbolische Schreibweise mit Faltungsstern |

|
| Gleichung 52 – Multiplikation im Frequenzbereich |
Werden
zwei Frequenzfunktionen X1(ω) und X2(ω) miteinander gefaltet,
entspricht das der Produktbildung ihrer Fourierrücktransformierten im
Zeitbereich. Vergleiche Gleichungen (53) und (54). Wir werden später
genauer auf Anwendungen der Faltung eingehen. An dieser Stelle wollen
wir als Merksatz knapp zusammenfassen:
Faltung im
Zeitbereich entspricht Multiplikation im Frequenzbereich bzw.
Multiplikation im Zeitbereich entspricht Faltung im Frequenzbereich.
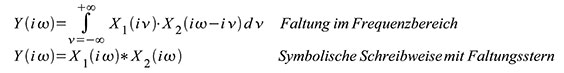
|
| Gleichung 53 – Faltung im Zeitbereich und symbolische Schreibweise mit Faltungsstern |

|
| Gleichung 54 – Multiplikation im Frequenzbereich |
Von der Faltungssumme zum Faltungsintegral
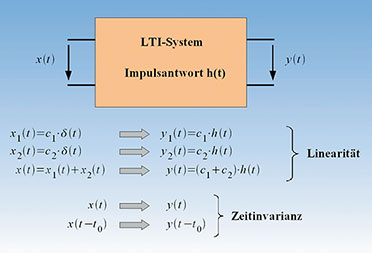
|
| Bild 21: Die Eigenschaften eines LTI-Systems: linear und zeitunabhängig |
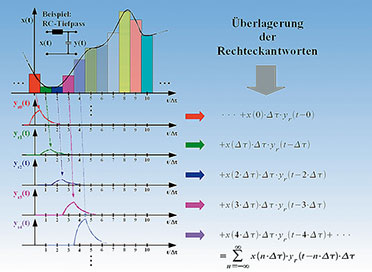
|
| Bild
22: Die Überlagerung der Systemantworten auf eine durch eine Folge von
Rechtecken nachgebildete Eingangsfunktion führt zur Faltungssumme als
Ausgangsfunktion |
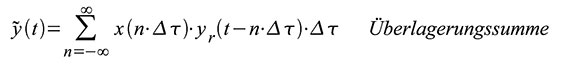
|
| Gleichung 55 – Überlagerungssumme |
Je
feiner nun die Treppe gestuft wird, umso ähnlicher wird die
Überlagerungssumme dem wahren Ausgangssignal des Systems. Im
Grenzübergang für Δτ → 0 gehen die Rechtecke des treppenförmigen
Eingangssignals xr(t) in eine unendliche Rechteckdauer Δτ zum
infinitesimal kurzen Zeitabschnitt dτ, die Summe zum Integral und die
diskreten Zeitpunkte nΔτ zur Laufvariablen τ wie in (56) und (57). Die
Gleichung (56) ist nichts weiter als die bereits aus Gleichung (22)
bekannte Ausblendeigenschaft des δ-Impulses. Gleichung (57) ist das
Faltungsintegral aus dem Eingangssignal und der Impulsantwort des
Systems. Wegen der LTI-Eigenschaften genügt es also, die Antwort y(t) =
h(t) des Systems auf einen Dirac-Impuls δ(t) als Eingangssignal zu
kennen. Für ein beliebiges Eingangssignal x(t) folgt dann aus Gleichung
(57) die entsprechende Ausgangsspannung y(t) = x(t)*h(t). 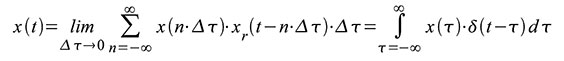
|
| Gleichung 56 |
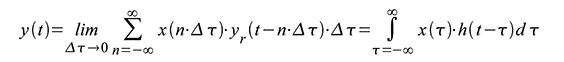
|
| Gleichung 57 |
Eine
erstaunliche Tatsache! Es ist sehr nützlich, einige der wichtigsten in
den Gleichungen (58–62) dargestellten Eigenschaften der Faltung zu
kennen. Die meisten davon lassen sich unmittelbar aus dem
Definitionsintegral nach Gleichung (51) oder (57) herleiten. 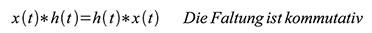
|
| Gleichung 58 – Die Faltung ist kommutativ |
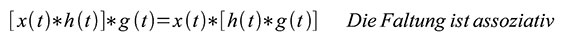
|
| Gleichung 59 – Die Faltung ist assoziativ |
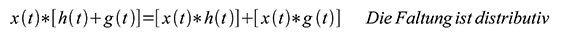
|
| Gleichung 60 – Die Faltung ist distributiv |
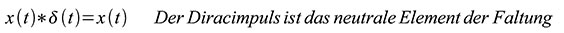
|
| Gleichung 61 – Der Diracimpuls ist das neutrale Element der Faltung |
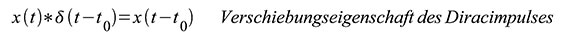
|
| Gleichung 62 – Verschiebungseigenschaften des Diracimpulses |
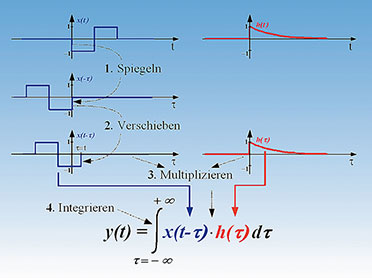
Grafische Veranschaulichung des Faltungsintegrals
|
| Bild 23: So werden das Eingangssignal x(t) und die Impulsantwort des Systems zum Ausgangssignal „gefaltet“ |
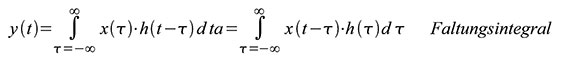
|
| Gleichung 63 – Faltungsintegral |
|
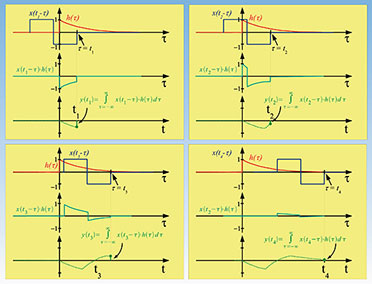
| Bild 24: Der Faltungsprozess zu vier aufeinanderfolgenden Zeitpunkten |
Wenn
wir nun auf Gleichung (50) unser Wissen anwenden, dass der Faltung im
Zeitbereich die Multiplikation im Frequenzbereich entspricht, führt dies
unter Auslassung einiger Zwischenschritte bei der Berechnung zu
Gleichung (64). Sie beschreibt nun nichts anderes als das mit der
Abtastkreisfrequenz ωs periodisch wiederholte Spektrum X(iω) der nicht
abgetasteten, bandbegrenzten Zeitfunktion x(t). Mit anderen Worten: Wird
eine Zeitfunktion x(t), deren Spektrum X(iω) ist, unter Einhaltung des
Abtasttheorems regelmäßig im Raster Ts = 2π/ωs abgetastet, so ist das
Spektrum Xs(iω) der abgetasteten Zeitfunktion eine in ωs periodische
Wiederholung von X(iω). Wir merken uns deshalb: Die Abtastung einer
Zeitfunktion führt zur Periodisierung ihres Spektrums. Wird das
Abtasttheorem eingehalten, überlappen sich die periodischen Spektren
nicht. Ist die Abtastfrequenz dagegen zu klein, überlagern sie sich.
Deshalb lässt sich aus ihnen die ursprüngliche Zeitfunktion nicht mehr
fehlerfrei zurückgewinnen. 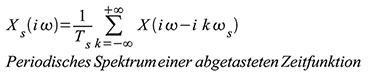
|
| Gleichung 64 – Periodisches Spektrum einer abgetasteten Zeitfunktion |
|
| Bild
25: Wird das Abtasttheorem verletzt, überlagern sich die periodischen
Spektren und das Spektrum des unabgetasteten Originalsignals lässt sich
nicht wiedergewinnen. Es ist durch Aliasanteile verfälscht. |
Fassen
wir also noch einmal zusammen: Durch das Abtasten eines bandbegrenzten
Signals entstehen bei Vielfachen der Abtastfrequenz Kopien des
ursprünglichen Spektrums des unabgetasteten Signals (Aliasspektren). Die
Betrachtung der Grenzfälle ist interessant. Lassen wir das
Abtastintervall gegen null gehen, entnehmen wir also mit einer unendlich
hohen Abtastfrequenz Signalproben, schieben sich die Aliasspektren ins
Unendliche und es verbleibt das Basisbandspektrum des unabgetasteten
Signals. Verringern wir die Abtastfrequenz dage gen immer mehr, rücken
die periodischen Spektren immer weiter zusammen. Mit dem Verletzen des
Abtasttheorems beginnen sie sich zu überlagern, bis sie im Grenzfall
eines einzigen Abtastwerts den konstanten Summenwert 1 annehmen (65). 
|
| Gleichung 65 |
In Teil 4 beschäftigen wir uns mit der Digitalisierung analoger Signale. Fachbeitrag als PDF-Download herunterladen
Inhalt
Sie erhalten den Artikel in 1 Version:
 als PDF (6 Seiten)
als PDF (6 Seiten)
Sie erhalten folgende Artikel:
- Einführung in die digitale Signalverarbeitung Teil 3/8
| weitere Fachbeiträge | Foren | |
Hinterlassen Sie einen Kommentar:






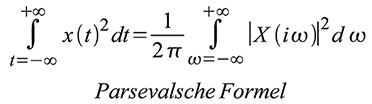
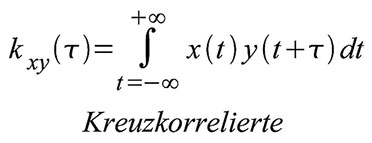
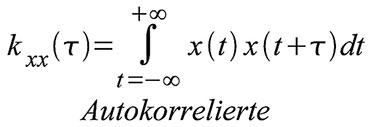

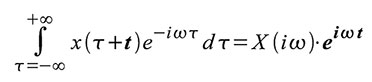
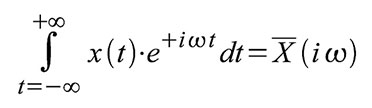
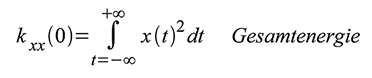
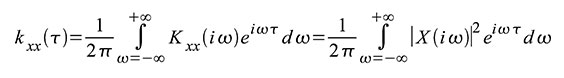



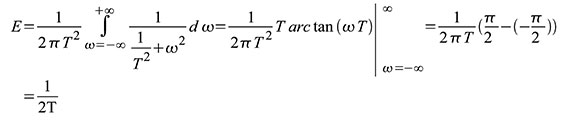


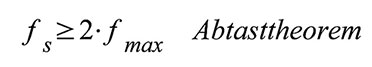

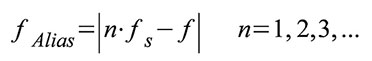
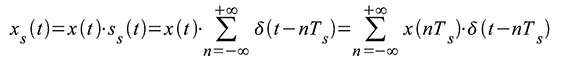
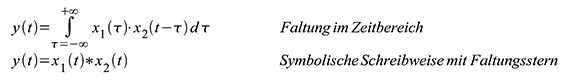

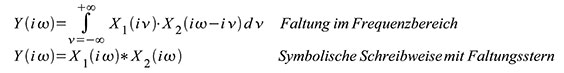



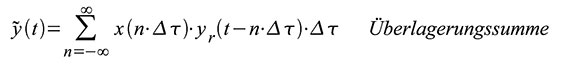
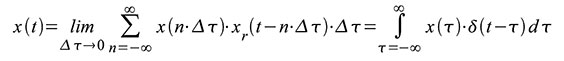
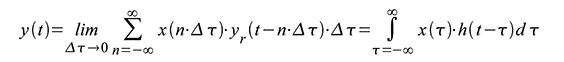
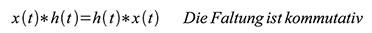
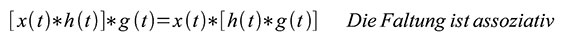
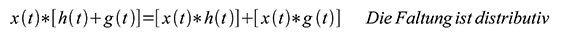
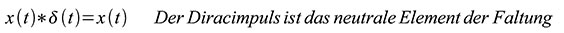
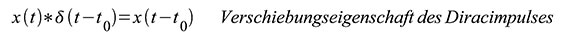

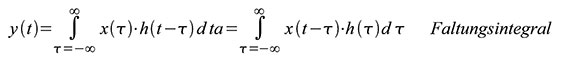

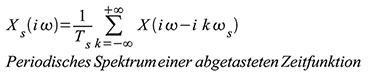


 als PDF (6 Seiten)
als PDF (6 Seiten)