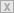Einführung in die digitale Signalverarbeitung Teil 4/8
Aus ELVjournal
05/2007
0 Kommentare
Der Abtastvorgang in der Praxis
|
| Bild 26: Der Name ist Programm: Sample&Hold (Abtasten und Halten) |
|
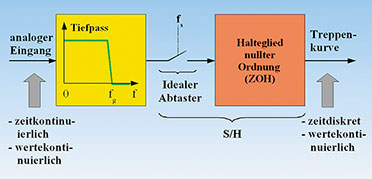
| Bild 27: Der reale Abtaster hält den Abtastwert über ein Abtastintervall. |
Impulsantwort und Frequenzgang eines ZOH

|
| Bild 28: Die Impulsantwort eines Haltegliedes nullter Ordnung (ZOH) ist ein Rechteck von der Dauer eines Abtastintervalls. |
|
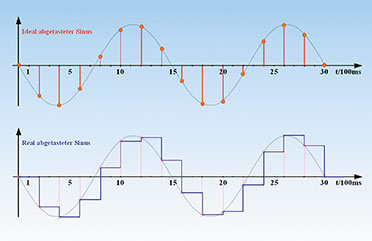
| Bild 29: Der Frequenzgang eines ZOHs nach Betrag und Phase |
|
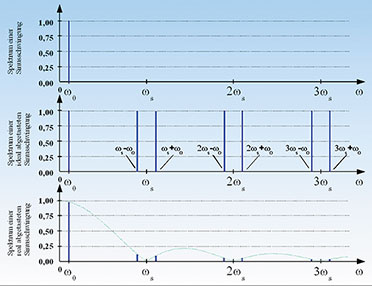
| Bild 30: Die periodischen Spektren einer abgetasteten Funktion werden an den Nullstellen des ZOH-Frequenzgangs gestaucht. |
|
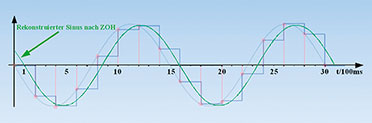
| Bild 31: Nach dem ZOH ist der rekonstruierte Sinus leicht in der Amplitude reduziert und verzögert. |
Von der Treppenkurve zum Digital-Signal
Die
Treppenkurve hinter dem Abtast-Halteglied ist wertekontinuierlich. Die
Stufenhöhe entspricht der Veränderung des Sig nalwerts von einem
Abtastzeitpunkt zum nächsten. Dennoch ist die Treppenkurve kein getreues
Abbild des Analog- Signals. Zu Beginn einer Stufe haben Treppe und
Signal den gleichen Wert. Weil während des Abtastintervalls dieser Wert
vom ZOH gehalten wird, bildet sich im Lauf des Abtastintervalls ein
zunehmender Fehler. Dieser Fehler hat also seine Ursache in der
Diskretisierung der Zeit. In einem digitalen Signalverarbeitungssystem
wird bekanntlich mit Binärzahlen (Folgen aus Nullen und Einsen = Wort)
gerechnet. Deren Länge ist in der Praxis begrenzt, wodurch sich nur eine
endliche Anzahl von Werten darstellen lässt. Dies ist eine
Diskretisierung der Amplitudenwerte. Dazu muss die Stufenhöhe der
Treppenkurve in ein Raster gebracht werden, dessen Feinheit von der
Wortlänge vorgegeben wird. Diesen Vorgang nennt man Quantisierung.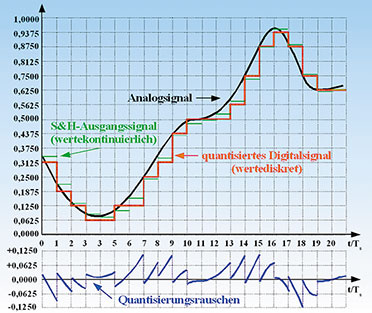
|
| Bild 32: Durch das Darstellen des ZOH-Ausgangssignals mit endlicher Genauigkeit entsteht ein Quantisierungsfehler. |
Analog-zu-digital-Wandler
In
der Praxis übernimmt der Analog-Digital-Wandler (A/DWandler, ADC:
Analogue to Digital Converter) die Funktion des Quantisierens. Sein
analoger Eingang wird mit dem Ausgangssignal des S&H-Glieds gespeist
(grüne Treppenkurve). Im Laufe der Abtastperiode muss das mit der
Stufenhöhe am besten korrespondierende Binärwort berechnet werden. Damit
wird die Folge der grünen Stufen in Abbildung 32 in eine Folge von
Binärzahlen entsprechend den roten Stufen umgewandelt.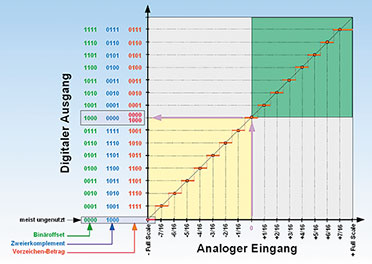
|
| Bild 33: Die Kennlinie eines A/D-Wandlers beschreibt, wie analoge Eingangswerte in digitale Ausgangswörter umgesetzt werden. |
Digitale Zahlenformate
Computer
arbeiten mit Zahlendarstellungen, die nur aus den Ziffern 0 und 1
bestehen und deshalb als zweiwertig, dual oder binär bezeichnet werden.
Wir wollen uns nur knapp und übersichtsartig mit den wichtigsten
Darstellungsformen beschäftigen. Das duale Zahlensystem gehört wie auch
das Dezimal- oder das Hexadezimalsystem zur Klasse der polyadischen
Zahlensysteme. Das bedeutet, dass jede endliche reelle Zahl als Summe
von Potenzen einer ganzzahligen Basis B dargestellt werden kann.
Gleichung (67) zeigt dies. Am Beispiel für die dezimale Zahl 49,375
(Basis B = 10, Koeffizienten 0 ≤ ξ ≤B – 1 = 9) sei dies in Gleichung
(68) erläutert. Die Darstellung als duale Zahl in Gleichung (69) erfolgt
genau gleich, außer dass die Basis jetzt B = 2 ist und die
Koeffizienten nur den Wert 0 oder 1 annehmen können.Zur
Vereinfachung kann man nun nur noch die Koeffizienten anschreiben und
durch das Komma anzeigen, ab wo die Hochzahlen der Potenzen negativ
sind. Aus Gleichung (69) wird dann Gleichung (70). Bei ganzen Zahlen
fallen die Potenzen mit negativen Hochzahlen weg, das Komma und was
rechts davon steht, kann gestrichen werden. Wir haben es dann mit einer
vorzeichenlosen Ganzzahl (Unsigned Integer) oder Festkommazahl zu tun.
Zur Terminologie: Die Koeffizienten der Potenzen mit den möglichen
Werten 0 oder 1 werden als Bits bezeichnet. Der Koeffizient der größten
Potenz heißt MSB (Most Significant Bit = höchstwertiges Bit) und steht
im Bitmuster ganz links. Der Koeffizient der kleinsten Potenz heißt LSB
(Least Significant Bit = niedrigstwertiges Bit) und steht im Bitmuster
ganz rechts. 8 Bits fasst man zu einem Byte (auch 8-Bits-Wort genannt)
zusammen und ein Byte wiederum besteht aus zwei Halbbytes (4-Bits-Wort),
den Nibbles. Die höherwertigen linken vier Bits bilden das „upper
nibble“, die rechten das „lower nibble“. 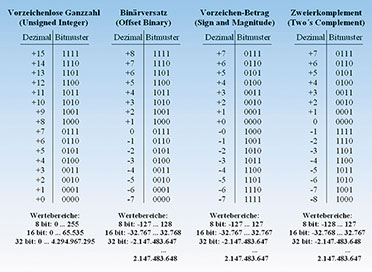
|
| Bild 34: Eine Übersicht über die wichtigsten Darstellungsformen für Binärzahlen |
Vorzeichenlose Ganzzahl (Unsigned Integer)
Hier
wird einfach von null ausgehend hochgezählt. Negative Zahlen können
nicht dargestellt werden. Die Umwandlung in eine Dezimalzahl (oder eine
Zahl mit einer anderen Basis als 10) ist einfach durch Anwendung von
Gleichung (67) möglich.Binärversatz (Offset Binary)
Wie Unsigned Integer, aber gegen die dezimalen Werte so verschoben, dass auch negative Zahlen darstellbar sind.
Vorzeichen-Betrag (Sign and Magnitude)
Hier
wird ganz einfach das MSB als Vorzeichen (0: positiv, 1: negativ) und
der rechts davon stehende Rest als Betrag interpretiert. Dadurch
„verschwendet“ man eine Ziffer, denn es entstehen eine positive Null
(0000) und eine negative Null (1000).Zweierkomplement (Two's Complement)
Diese
Darstellungsform ist in der digitalen Signalverarbeitung und in
modernen Computern mit Abstand am beliebtesten. Das ist in der einfachen
Art begründet, mit der sich Additionen und Subtraktionen hardwaremäßig
ausführen lassen. Eine einfache Analogie ist der Walzenmechanismus eines
Kilometerzählers in einem älteren Tachometer. Steht er auf null und man
fährt in Vorwärtsrichtung los, wird er anzeigen „0000, 0001, 0002,
0003, …“. Beim Rückwärtsfahren dagegen wird man ablesen „0000, 9999,
9998, 9997, …“. In binärer Darstellung führt das bei den positiven
Zahlen zu 0000, 0001, 0010, 0011, …“ bzw. „0000, 1111, 1110, 1101, …“.
Diesen Zählmechanismus findet man in den aus Flipflops bestehenden
Rechenregistern eines Computers wieder, was ihn so geeignet für die
Maschine macht. Beim Rückwärtszählen aus dem positiven Bereich erfolgt
der Übergang zu den negativen Zahlen einfach durch einen Überlauf 0000 →
1111. Die Interpretation der Zahl ist damit ganz einfach: Das MSB
bestimmt die Polarität (MSB = 0: positiv, MSB = 1: negativ). Bei den
positiven Zahlen wird der Rest des Bitmusters als Betrag bestimmt, bei
den negativen Zahlen wird der Rest des Bitmusters invertiert (0 → 1, 1 →
0) und 1 dazuaddiert, das Ergebnis wird (ohne MSB!) als Betrag der
negativen Zahl interpretiert. Zum Beispiel +7 → –7 entspricht 0111 →
1000 + 0001 = 1001. Addition und Subtraktion führen in
Zweierkomplementdarstellung ohne weitere Korrekturen zum richtigen
Ergebnis. Ein Beispiel: +5 – 7 = +5 + (–7) = –2 → 0101 + 1001 = 1110Gleitkommazahlen (Floating Point Numbers)
Das
binäre Gleitkommazahlenformat lässt die Darstellung erheblich größerer
Wertebereiche zu. Etwas Ähnliches kennen wir von dem wissenschaftlichen
Zahlenformat eines Taschenrechners, der mit Dezimalzahlen rechnet. Wenn
auf seinem Display z. B. die beiden Zahlen –2,746 (Mantisse) und 09
(Exponent) erscheinen, haben wir es mit dem Produkt aus der negativen
Zahl –2,746 und der Zehnerpotenz 109 = 1.000.000.000, d. h. mit
–2.746.000.000 zu tun.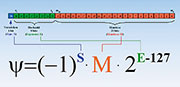
|
| Bild 35: Gleitkommazahlen decken mit 32 Bit einen riesigen Wertebereich ab. |
Gleichung
(72) stellt die Single-Precision-Gleitkommazahl als Binärzahl dar. Die
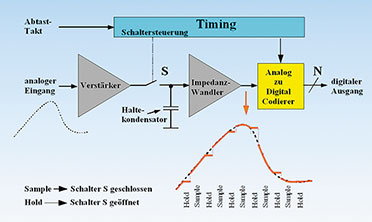
zwei Beispiele in Gleichung (73) sollen das verdeutlichen. Prinzipschaltung A/D-Wandler mit S&H
|
| Bild 36: Vom Speicherkondensator wird der Signalwert bis zum Ende des Abtastintervalls gehalten. |
Veranschaulichung der Diskretisierung von Zeit und Amplitude
Anhand
der folgenden drei Abbildungen wollen wir die Auswirkungen der
Rasterung (Diskretisierung) von Zeit (Abtastfrequenz) und Amplitude
(Wertebereich) studieren. Dazu wurde in Scilab ein kleines Programm
geschrieben, welches eine vorgebbare analoge, d. h. werte- und
zeitkontinuierliche Zeitfunktion abtastet, den Abtastwert quantisiert
und den quantisierten Abtastwert über die Abtastperiode konstant hält.
Aus den Abweichungen zwischen der analogen kontinuierlichen Zeitfunktion
und der treppenförmigen werte- und zeitgerasterten wird der
Amplitudenfehler ermittelt.Wir
wählen als analoge Zeitfunktion eine exponentiell gedämpfte
Sinusschwingung über 2,5 Perioden (0…5 π = 15,7) gemäß Gleichung (74).
Die x-Werte werden als eine gewisse Zahl von Abtastwerten vorgegeben,
die Stufenhöhe über die Länge des darstellenden Binärwortes gesteuert.
Da wir einen y-Wertebereich von –1 ≤ y ≤ + 1 voraussetzen, beträgt bei
einer Wortlänge von w das Quantisierungsraster 2-w+1. In
Abbildung 37 wurde eine Wortlänge von w = 5 gewählt, deshalb ist die
Stufenhöhe der Treppenkurve 2-5+1 = 2-4 = 0,0625. Weil mit nur 50
Abtastwerten über das ganze Intervall 0…5 π gearbeitet wird, ergibt sich
eine recht grobe Kurve des Quantisierungsfehlers. In Abbildung 38
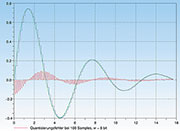
beträgt die Wortlänge w = 8, deshalb ist die minimale Stufenhöhe der
Treppenkurve 2-7 = 0,0078125. Das Funktionsintervall wird 100-mal
abgetastet. Im Ergebnis ist der Quantisierungsfehler kleiner als in
Abbildung 37. Wegen des relativ groben zeitlichen Abtastrasters ergeben
sich aber dort, wo die analoge Funktion steil ist (d. h. ihre Werte in
kurzer Zeit stark verändert), immer noch zeitbedingte große Fehler von
einem Vielfachen des Quantisierungsintervalls. Wenn man sowohl die
Abtasthäufigkeit als auch die Wortlänge weiter steigert, gehen die damit
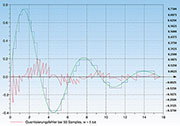
verbundenen Abbildungsfehler weiter zurück. Abbildung
39 zeigt die Verhältnisse bei 5000 Abtastwerten und 32 Bit Wortbreite.
Durch die extrem feine Stufung der Treppenkurve ist diese praktisch
deckungsgleich mit der analogen Kurve. Erst bei starker Vergrößerung
zeigen sich die Abweichungen. Entsprechend klein sind auch die
Quantisierungsfehler. Sie sind in diesem extremen Beispiel sicherlich
kleiner als das jedem analogen Signal überlagerte mehr oder weniger
starke Rauschen. An den flachen Teilen der Kurve lässt sich die hohe
Amplitudenauflösung gut erkennen. Abbildung
40 zeigt dies an der Umgebung des dritten Maximums. Zusammenfassend:
Sowohl die wortbreitenbedingte Amplitudenauflösung als auch die zur
Abtastfrequenz proportionale Zeitauflösung gehen im Zusammenwirken mit
der Signalform in den Quantisierungsfehler ein. Bei
linearer Quantisierung (gleiche Stufenhöhe für alle Signalwerte) wird
der Aussteuerbereich A (– Full Scale … + Full Scale) in 2w gleich große
Quantisierungsintervalle Δ zerlegt, wobei w die Wortlänge eines
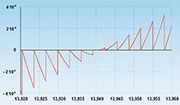
Abtastwerts in Bits beschreibt (Gleichung [75]). Der Quantisierungs-
bzw. Rundungsfehler ε in einem Abtastintervall Ts ist definiert als der
Unterschied zwischen wahrem und quantisiertem Abtastwert (76). 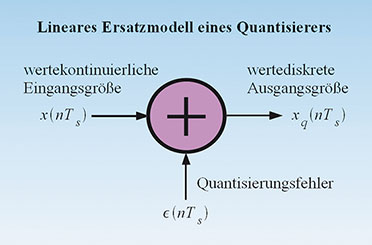
|
| Bild
41: Das lineare Ersatzmodell eines Quantisierers fügt dem
wertekontinuierlichen Signal nach dem ZOH eine rauschartige Störgröße
hinzu, die den Quantisierungsfehler repräsentiert. |
Wegen
des sprunghaften Verhaltens des Quantisierers an den
Entscheidungsschwellen zählt er zu den nichtlinearen Elementen. Man kann
ihn aber durch ein lineares Ersatzmodell nachbilden (Abbildung 41). Das
Quantisierungsrauschen wird über das Signal-Rausch- Verhältnis nach
Gleichung (77) beschrieben: Dabei stellen Px die Signalleistung am
Eingang des Quantisierers und Pε die Leistung des Quantisierungsfehlers
dar. Setzt
man voraus, dass die Quantisierungsfehler unkorrelierte, im Intervall
[–Δ/2, Δ/2] gleich verteilte Zufallsgrößen sind und die
Quantisierungsfehler ε(nTs) nicht von den wertekontinuierlichen
Eingangsabtastwerten x(nTs) abhängen, ergibt sich die Leistung des
gleichspannungsfreien Quantisierungsfehlers ε(nTs) gemäß Gleichung (78). Mit
der Definition des Quantisierungsintervalls nach Gleichung (75) wird
aus Gleichung (78) die (79). Gleichung (79) in Gleichung (77)
eingesetzt, ergibt das gesuchte Signal-Rausch-Verhältnis in dB (80). Es
lohnt sich, Gleichung (80) etwas näher zu betrachten. Wir sehen, dass
der erste Summenterm auf der rechten Seite nur von der Wortbreite w
(also der Länge der darstellenden Binärzahl) abhängt. Jedes Bit mehr
erhöht den Signal-Rausch- Abstand um ca. 6 dB. Der zweite Summenterm
hängt von der Leistung des Eingangssignals des Quantisierers ab. Je
kleiner diese ist, desto kleiner wird der Rauschabstand. Andererseits
bewirkt ein großer Aussteuerbereich A ebenfalls eine Abnahme von S/N,
weil das Signal dann auf weniger Stufen quantisiert wird und die
relativen Quantisierungsfehler entsprechend größer werden. Bei
Vollaussteuerung mit einem Sinus ist der zweite Summenterm 1,76 dB, bei
typischen digitalen Audio-Signalen –8,5 dB. Audio-CDs mit einer
Wortbreite w = 16 Bit können deshalb maximal ein S/N von 96,3 – 8,5 =
87,8 dB erreichen. Diese Betrachtungen setzen ein unverrauschtes
Eingangssignal voraus. Für das Quantisierungs- oder Rundungsrauschen gut
ausgesteuerter A/D-Wandler mit Wortlängen von mehr als 8 Bit merken wir
uns als Faustregel: 6 dB S/N pro Bit Wortlänge. In Teil 5 beschäftigen
wir uns mit den diskreten Berechnungsmethoden zur Faltung,
Fouriertransformation und ihrer schnellen Variante, der FFT. Fachbeitrag als PDF-Download herunterladen
Inhalt
Sie erhalten den Artikel in 1 Version:
 als PDF (7 Seiten)
als PDF (7 Seiten)
Sie erhalten folgende Artikel:
- Einführung in die digitale Signalverarbeitung Teil 4/8
| weitere Fachbeiträge | Foren | |
Hinterlassen Sie einen Kommentar:








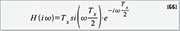






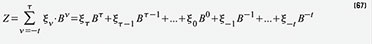
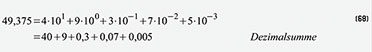
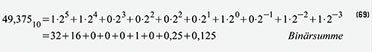




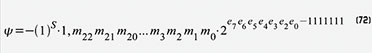





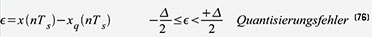


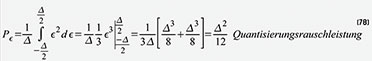
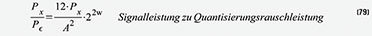

 als PDF (7 Seiten)
als PDF (7 Seiten)