Einführung in die digitale Signalverarbeitung Teil 5/8
Aus ELVjournal
06/2007
0 Kommentare
Diskrete Berechnungsmethoden
Wenn
wir eine ursprünglich kontinuierliche Zeitfunktion in eine Folge von
Binärzahlen verwandelt haben, benötigen wir zu deren weiterer
Verarbeitung mathematische Werkzeuge: die diskreten Varianten der
Fouriertransformation, Faltung, Korrelation, Integration usw. Zum Glück
lassen sich nahezu alle Formeln mit leichten Anpassungen aus der
kontinuierlichen Welt in die „gequantelte“ übernehmen. Die deutlichsten
Unterschiede: Ein Integral wird zur Summe und die kontinuierliche Zeit t
zu Vielfachen der Abtast periode n • Ts. Bei unseren weiteren
Betrachtungen vernachlässigen wir zunächst den unvermeidlichen
Amplitudenfehler bei der Darstellung eines Signalwertes y(t) durch
seinen Abtastwert y(n • Ts). Gleichung 81 zeigt, wie der Wert y zu einem
beliebigen Zeitpunkt t (Momentanwert) in ein zeitliches Raster n • Ts
gebracht wird. Zur einfacheren Anschrift ersetzen wir n • Ts durch n.
Bei der Darstellung von y(n) entsteht somit aus einem kontinuierlichen
Kurvenverlauf eine Impulsfolge von diskreten Werten zu den Zeitpunkten n
• Ts, wie sie Abbildung 42 darstellt. Die in Abbildung 42 abgebildeten
Folgewerte drückt Gleichung (82) aus.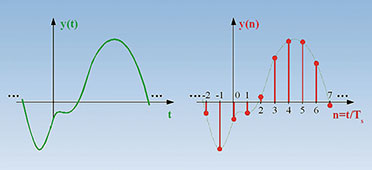
|
| Bild
42: Durch Abtastung werden dem zeitkontinuierlichen Signal zu diskreten
Zeitpunkten t = n • Ts Werte zur weiteren mathematischen Verarbeitung
entnommen. |
Diskrete Faltung
Ebenso
wie bei den kontinuierlichen Systemen ist auch ein LTI-Abtastsystem
(LTI: linear, zeitinvariant) durch seine Impulsantwort h(n) vollständig
charakterisiert. Die Faltung eines beliebigen Eingangssignals x(n) mit
der Impulsantwort h(n) ergibt deshalb das Ausgangssignal y(n). Die
Faltung ist kommutativ, was durch die zwei Anschriften der Faltungssumme
in Gleichung (83) zum Ausdruck kommt.An
einem Beispiel wollen wir die Faltung noch einmal veranschaulichen. In
Tabelle 2 wird von einem System ausgegangen, welches auf den
Einheitsimpuls δ(n) an seinem Eingang mit der Impulsantwort h(n) am
Ausgang reagiert. Die Wertefolge von δ(n) hat nur bei n = 0 den Wert 1
und ist zu allen anderen Zeiten n ≠ 0 null. Die Impulsantwort besteht
aus vier Werten ungleich null, nämlich h(0) = 1, h(1) = 0,75,h(2) = 0,5
und h(3) = 0,25. Nun geben wir ein Signal x(t) auf den Eingang, welches
aus drei Werten ungleich null besteht. Diese sind x(0) = –1, x(1) =
–0,5, x(2) = –0,25. Auf jeden einzelnen dieser Eingangsimpulse reagiert
das System gemäß seiner Impulsantwort und in der Überlagerung der
Einzelimpulsantworten ergibt sich das Ausgangssignal als Reaktion auf
die Eingangsfolge. 
|
| Tabelle 2: In der Tabelle sind alle Zahlenwerte für das Bestimmen einer Faltungssumme zum Nachvollziehen eingetragen. |
In
Abbildung 43 ist die Aussage der Tabelle grafisch dargestellt. Wir
sehen, dass die drei Eingangsimpulse zu drei verschobenen und bewerteten
Impulsantworten (blau, grün und türkis) führen. Dabei beginnt keine der
Impulsantworten vor dem anregenden Eingangsimpuls. Solche Systeme nennt
man kausal, denn sie funktionieren nach dem Grundsatz: „keine Wirkung
ohne und vor einer Ursache“. Die Summe ist das Ausgangssignal als
Ergebnis der Faltung der Eingangsfolge mit der Impulsantwortfolge des
Systems. Die Faltungssumme kann mit einem Tabellenkalkulationsprogramm
wie Microsoft Excel oder OpenOffice Calc leicht berechnet werden. So ist
auch Tabelle 2 entstanden. Noch einfacher ist die Berechnung mit dem
bereits erwähnten Programm Scilab. Hier braucht man nur die von null
verschiedenen Impulsfolgenabschnitte von x(n) und h(n) und den
Faltungsbefehl wie bei einem Taschenrechner einzugeben. Abbildung
44 zeigt den zugehörigen Screenshot. Aber auch ein kleines Programm zur
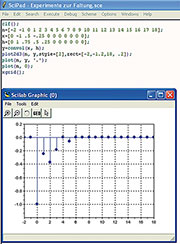
Durchführung der Faltung und grafischen Darstellung des Ergebnisses ist
schnell geschrieben, wie Abbildung 45 beweist. Die Beispiele sollen
Lust machen, sich doch mit dieser extrem nützlichen, kostenlosen
Software etwas zu beschäftigen. Es lohnt sich auf jeden Fall! 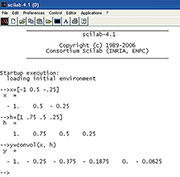
|
| Bild 44: Scilab als eine Art wissenschaftlicher Taschenrechner „faltet“ mit geringstem Aufwand. |
|
| Bild 45: Auch die grafische Darstellung des Faltungsergebnisses erfordert nur wenige Zeilen Scilab-Programmcode. |
Wichtig
ist die Erkenntnis, dass bei der Faltung zweier begrenzter Folgen auch
das Faltungsresultat begrenzt ist. Wie Gleichung (84) zeigt, ist das
Ausgangssignal immer so lang (Ly) wie die Summe der Längen von
Impulsantwort (Lh) und Eingangssignal (Lx) minus 1. In unserem Beispiel
ist die Impulsantwort 4 Abtastwerte lang, das Eingangssignal 3
Abtastwerte, also muss die Ausgangsfolge aus 4 + 3 – 1 = 6 Abtastwerten
bestehen. Das bedeutet natürlich im Umkehrschluss, dass wir mit
Ausschnitten der Impulsantwort und der Eingangsfunktionen rechnen
müssen, um keine unendlich lange Ausgangsfolge zu erhalten. Diesem Zweck
dient die „Fensterung“ (Multiplikation mit einer Rechteckfunktion), mit
deren Auswirkung wir uns später auseinandersetzen wollen. Die Kunst
besteht darin, das Fenster so zu wählen, dass man mit angemessenem
Rechenaufwand die Lösung mit der gewünschten Genauigkeit erhält. Eine
kleine Erkenntnis am Rande. Aus dem analogen Bereich wissen wir, dass
die Fouriertransformierte einer Rechteck Zeitfunktion eine si-Funktion
im Frequenzbereich ist. Eine Dreiecks-Zeitfunktion hat dagegen im
Frequenzbereich das Quadrat zweier si-Funktionen zur Folge. Das Spektrum
ist also immer positiv. Warum? Der Grund ist, dass die Dreiecksfunktion
aus der Faltung zweier Rechtecke hervorgeht. Abbildung 46 demonstriert
das über ein kleines Scilab-Programm, Abbildung 47 zeigt, dass eine
ähnliche Darstellung auch mit OpenOffice Calc zu erhalten ist. 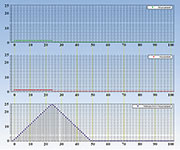
|
| Bild 46: Die Faltung zweier Rechtecke ergibt ein Dreieck (Beispiel mit Scilab gerechnet). |
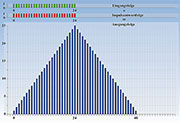
|
| Bild 47: Mit OpenOffice Calc erhält man das gleiche Ergebnis wie in Bild 46. |
Im
Frequenzbereich werden die Spektren der gefalteten Rechtecke – zwei
si-Funktionen – miteinander multipliziert. Ihre negativen Abschnitte
sind deshalb nach dem Quadrieren positiv. Wir können das später mit der
diskreten Fouriertransformation (DFT) am praktischen Beispiel
nachvollziehen. Noch ein Beispiel für die Nützlichkeit des
Überlagerungsprinzips (Superpositionsprinzip), welches bei LTI-Systemen
angewandt werden darf. Nehmen wir an, wir hätten ein System mit
bekannter Impulsantwort und einem Eingangssignal, welches aus 6
Abtastwerten mit +1 (positives Rechteck) und darauf folgend 6
Abtastwerten mit –1 (verzögertes negatives Rechteck) besteht. Wenn wir
die Systemantwort auf das positive Rechteck bereits kennen, ist uns auch
die Systemantwort auf das negative, verzögerte Rechteck bekannt. Sie
ist nichts weiter als die invertierte und um 6 Abtastintervalle
verzögerte (nach rechts verschobene) Systemantwort auf das positive
Rechteck. Diese „negative“ Systemantwort mit der „positiven“ überlagert,
ergibt das gewünschte Resultat. Allgemein gilt: Wenn sich eine
komplizierte Eingangsfunk tion eines Systems in einfachere Bestandteile
zerlegen lässt, kann man die Antworten eines LTI-Systems darauf
(Abbildung 48) ermitteln und zur Systemantwort auf die unzerlegte,
komplizierte Eingangsfunktion (Abbildung 49) überlagern. Das vereinfacht
die Lösung eines Problems oft erheblich. Solche „divide and
conquer“-Methoden (teile und herrsche) werden in vielen Bereichen der
Mathematik und Naturwissenschaften angewandt. 
|
| Bild 48: Zwei Eingangssignale führen zu je einem Ausgangssignal. |

|
| Bild
49: Die Überlagerung der zwei Eingangssignale aus Bild 48 führt zur
Überlagerung der beiden Ausgangssignale. Das ist ein Charakteristikum
von LTI-Systemen. |
Diskrete Fouriertransformation
Das
aus der analogen Signaldarstellung bekannte Fourierintegral dient der
Transformation einer Zeitfunktion in den Frequenzbereich (Zeitfunktion
¡ú Spektrum), das inverse Fourierintegral der R¨¹cktransformation in den
Zeitbereich (Spekt rum ¡ú Zeitfunktion). Ohne Herleitung geben wir die
aus den Gleichungen (18) f¨¹r die Fouriertransformierte und (19) f¨¹r
die Fourierr¨¹cktransformierte von analogen Signalen die Beziehungen
f¨¹r zeitdiskrete (abgetastete) Signale an. Dabei wird noch
vorausgesetzt, dass nur ein endlich langer Abschnitt x(n) des Signals zu
transformieren ist, den man als eine Periode eines periodischen Signals
x (n) auffasst (Abbildung 50).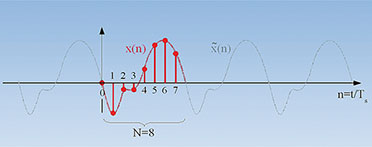
|
| Bild
50: Wenn ein mit der DFT zu transformierender Signalabschnitt eine
volle Periode des Signals darstellt, ist das Transformationsergebnis
exakt. |
|
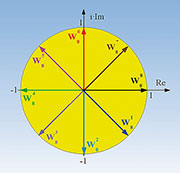
| Bild
51: Der Drehfaktor ist im wahrsten Sinn des Wortes Dreh- und Angelpunkt
der DFT und noch mehr ihrer schnellen Variante, der FFT. |
Die
Symmetrien bestehen darin, dass W88 = –W84, W87 = –W83, W86 = –W82 und
W85 = –W81 ist, also jeder Zeiger ein am Ursprung gespiegeltes
Gegenstück hat, dessen Real- und Imaginärteil ein inverses Vorzeichen
aufweist. Das Auswerten der Gleichung (85) von Hand mit Hilfe eines
Taschenrechners ist nicht schwierig, aber mühselig und fehlerträchtig.
Lediglich die erste Spektrallinie X(k = 0) ist einfach zu berechnen,
weil dann der Drehfaktor 1 ist und sich der Spektrallinienwert einfach
als Summe aller Abtastwerte ergibt. Entsprechendes gilt bei Gleichung
(86). Mit einem kleinen Scilab-Programm kann man sich das Leben sehr
erleichtern. Abbildung 52 zeigt, wie ein diskretes Zeitsignal bestehend
aus 8 Abtastwerten gemäß Gleichung (85) in ein diskretes Spektrum aus
ebenfalls 8 Spektrallinien umgerechnet wird. Weil die Spektrallinien im
Allgemeinen komplex sind, wurde ihr Betrag berechnet und abgebildet.
Phaseninformationen sind dabei verloren gegangen. In Teil 6 studieren
wir die Auswirkungen des Auffüllens von Folgen mit Nullwerten im Zeit-
und Frequenzbereich („zero padding“), demonstrieren die diskrete Faltung
mit Hilfe der DFT und beschäftigen uns mit dem Radix-2-Algorithmus der
schnellen Fouriertransformation (FFT). 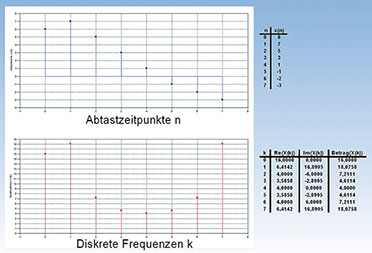
|
| Bild 52: Die Berechnung der DFT nach Gleichung (85) von Hand ist stupide und mühsam, mit Scilab dagegen ganz einfach. |
Fachbeitrag als PDF-Download herunterladen
Inhalt
Sie erhalten den Artikel in 1 Version:
 als PDF (6 Seiten)
als PDF (6 Seiten)
Sie erhalten folgende Artikel:
- Einführung in die digitale Signalverarbeitung Teil 5/8
| weitere Fachbeiträge | Foren | |
Hinterlassen Sie einen Kommentar:



















 als PDF (6 Seiten)
als PDF (6 Seiten)