Einführung in die digitale Signalverarbeitung Teil 6/8
Aus ELVjournal
01/2008
0 Kommentare
Rückblick
Es
wurde bereits gesagt, dass die diskrete Fouriertransformation eine
gewisse Anzahl von Zeitwerten in ebenso viele Spektralwerte überführt.
Bei der Wahl von N als der Anzahl von Abtastwerten sollte die Messdauer N
• Ts mindestens gleich lang wie die Signaldauer sein, um dieses
vollständig zu erfassen. Wenn wir N dann noch als Zweierpotenz (2, 4, 8,
16 ..., 1024 ...) wählen, ist das Verfahren der schnellen
Fouriertransformation (Fast Fourier Transform: FFT) anwendbar. Weil die
spektrale Auflösung umgekehrt proportional zur Anzahl der Abtastwerte
ist (siehe Gleichung [87]), sollte N möglichst groß sein. Das kann durch
eine häufigere Abtastung des zeitkontinuierlichen Signals geschehen
oder durch das Anhängen von Nullen an die verfügbare Folge von
Abtastwerten. Letzteres wird als Time Domain Zero Padding (TDZP)
bezeichnet und bewirkt die Interpolation zusätzlicher Spektralwerte.
Umgekehrt führt das Einfügen von Nullen (Frequency Domain Zero Padding:
FDZP) in der Mitte der Spektralfolge zu interpolierten Zeitfolgenwerten.Time Domain Zero Padding
Schauen
wir uns die Wirkung des Anhängens von Nullen an eine Signalfolge im
Zeitbereich einmal genauer an. Im Englischen wird das als Time Domain
Zero Padding (TDZP) bezeichnet, was in der Übersetzung so viel heißt
wie: Auffüllen mit Nullen im Zeitbereich. Die aufgefüllte Folge wird
dann der DFT unterworfen, d. h., in den Frequenzbereich transformiert.
Da die Zahl der Spektrallinien immer gleich der Anzahl der
transformierten Zeitfolgenwerte ist, erwarten wir also ein feiner
gerastertes Linienspektrum, d. h. die spektrale Auflösung muss steigen.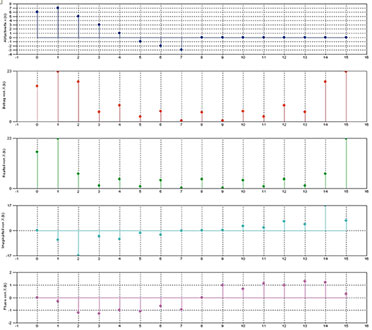
|
| Bild
53: Das Erweitern der Zeitsignalfolge durch Anhängen von Nullen (hier
8) führt im Frequenzbereich zu interpolierten Spektralwerten. |
|
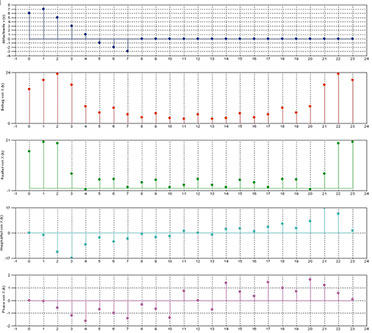
| Bild
54: Zwei angehängte Nullen pro Original-Zeitfolgenwert führen zu zwei
interpolierten Werten zwischen den Werten der Original-Spektralfolge. |
|
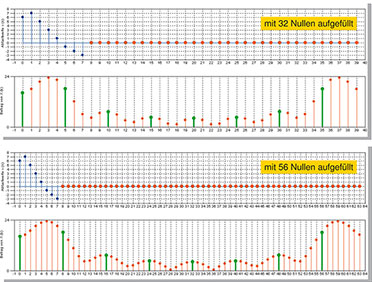
| Bild 55: Zero Padding im Zeitbereich mit 8 Signalwerten und 32 bzw. 56 Nullwerten. |
Frequency Domain Zero Padding

|
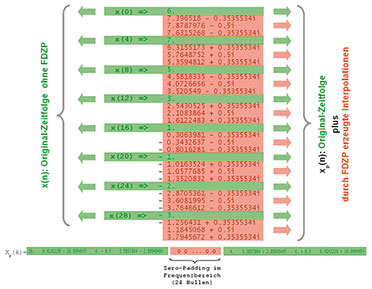
| Bild
56: Zero Padding im Frequenzbereich erfolgt durch Einfügen einer Folge
von Nullwerten in der Mitte der Original-Spektralfolge. Die Wirkung ist
das Einschachteln von interpolierten Werten zwischen die Werte der
Original-Zeitfolge. |
|
| Bild 57: Zereo Padding im Frequenzbereich (FDZP) zum Nachvollziehen |
Den
Zusammenhang zwischen Frequenzauflösung Δ, Frame- Länge T0 und
Samplingfrequenz fs = 1/Ts zeigt Gleichung 89. Durch das Zero Padding
verkleinern sich die Amplituden der transformierten Folgewerte, weil ja
die Signalenergie auf mehr Transformationsfolgewerte verteilt wird. Bei
Einfügen gleich vieler Nullen wie Signalfolgenwerte halbieren sich die
Amplituden der Transformationsfolge, bei doppelt so vielen Nullen gehen
sie auf ein Drittel zurück usw. In unseren Beispielen wurde deshalb mit
einem entsprechenden Faktor multipliziert, um die Originalwerte
einfacher in der interpolierten Folge wiederzufinden. 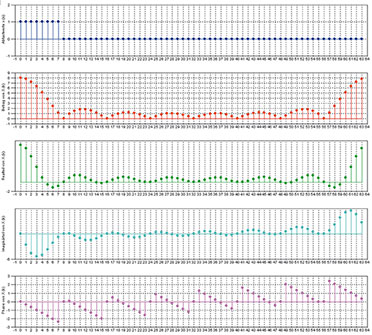
|
| Bild
58: Im Allgemeinen ist das Spektrum einer Zeitfolge durch einen Real-
und einen Imaginärteil oder seinen Betrag und seine Phase
gekennzeichnet. Das wird hier am Beispiel eines Rechtecks gezeigt. |
|
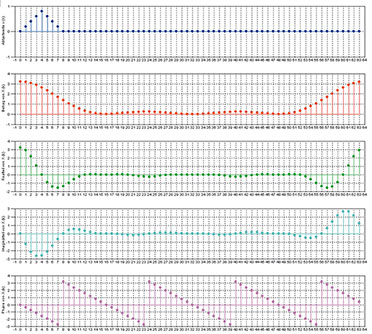
| Bild 59: Die DFT eines Dreiecks |
Diskrete Faltung mit Hilfe der DFT
Gleichung
83 definierte die Faltung zweier Zeitsignalfolgen. Eine war das
Eingangssignal und die andere die Impulsantwort eines LTI-Systems. Das
Faltungsergebnis ist das Ausgangssignal als Systemantwort auf das
Eingangssignal. Man kann das Ausgangssignal aber auch ohne Berechnung
der Faltungssumme bestimmen. Dazu werden die endlichen Zeitfolgen, die
x(n) mit der Länge N1 und h(n) mit der Länge N2 repräsentieren, mit so
vielen Nullen aufgefüllt, dass ihre Länge N ≥ N1 + N2 – 1 ist. Dann
werden die Folgen der DFT unterworfen, miteinander multipliziert und das
Produkt wird mit Hilfe der IDFT (inversen DFT) wieder in den
Zeitbereich zurücktransformiert. Wir haben damit die Faltung als
Operation im Zeitbereich über eine Multiplikation im Frequenzbereich
ausgeführt.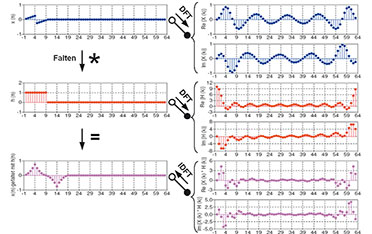
|
| Bild
60: Man kann zwei Zeitfolgen auch falten, indem man ihre diskreten
Fouriertransformierten miteinander multipliziert und das Produkt wieder
in den Zeitbereich zurücktransformiert (Convolution by DFT). |
Fachbeitrag als PDF-Download herunterladen
Inhalt
Sie erhalten den Artikel in 1 Version:
 als PDF (5 Seiten)
als PDF (5 Seiten)
Sie erhalten folgende Artikel:
- Einführung in die digitale Signalverarbeitung Teil 6/8
| weitere Fachbeiträge | Foren | |
Hinterlassen Sie einen Kommentar:











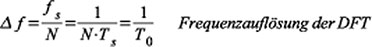



 als PDF (5 Seiten)
als PDF (5 Seiten)