Einführung in die digitale Signalverarbeitung Teil 8/8
Aus ELVjournal
03/2008
0 Kommentare
Die z-Transformation
Zur
Analyse digitaler Signale und Systeme (Abtastsysteme) im
Frequenzbereich hat sich die z-Transformation bewährt. Vor ihrer
Einführung wollen wir noch einmal einen Rückblick auf die Verhältnisse
im analogen kontinuierlichen Frequenzbereich werfen. Gleichung (18)
definierte die allgemeine Fouriertransformation eines beliebigen
Zeitereignisses. Nun nehmen wir als untere Integrationsgrenze t = 0 an
(kausale Zeitfunktion, die bei t = 0 beginnt) und ersetzen die imaginäre
Frequenzvariable iω durch die komplexe Frequenzvariable s = σ + iω. Die
Erweiterung der imaginären Frequenzvariablen iω um einen Realteil σ
wird analytische Fortsetzung genannt.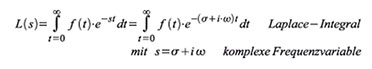
|
| Gleichung 103 |
|
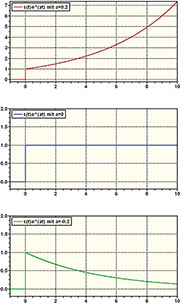
| Bild 67: Die Funktion eat klingt mit dem Dämpfungsfaktor a > 0 an, ist für a = 0 konstant und klingt für a < 0 ab. |
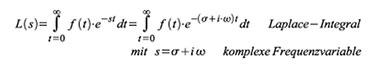
|
| Gleichung 103 |
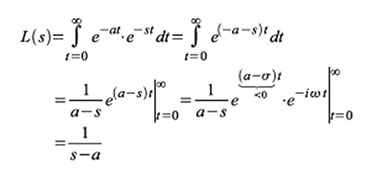
|
| Gleichung 104 |
|
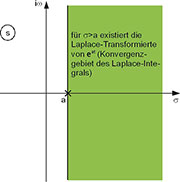
| Bild 68: Im grün eingefärbten Gebiet konvergiert das Laplace-Integral von eat. |
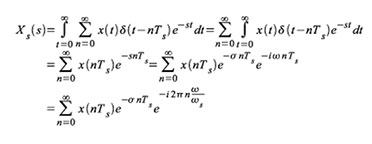
|
| Gleichung 105 |
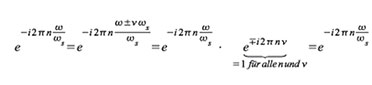
|
| Gleichung 106 |
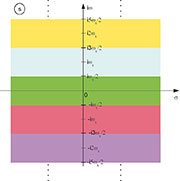
|
| Bild
69: Der gesamte Informationsgehalt eines bandbegrenzten, abgetasteten
Signals liegt in jedem einzelnen der abgebildeten Streifen in der
Spektralebene. Die Streifen wiederholen sich periodisch in ωs. Es genügt
daher, den grünen Streifen um den Ursprung zu betrachten. |
|
| Bild
70: Das Spektrum einer biquadratischen kontinuierlichen
Übertragungsfunktion muss bei ±ωs/2 bandbegrenzt werden, um Aliaseffekte
zu vermeiden. |
|
| Bild 71: Durch die Abtastung mit ωs wiederholt sich das Abtastspektrum periodisch in ωs. |
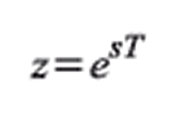
|
| Gleichung 107 |
Die
Abbildung z = esT bewirkt, dass die Teile jeden Streifens mit σ < 0
in Abbildung 69 deckungsgleich auf das Innere eines Einheitskreises in
der z-Ebene abgebildet wird. Für σ > 0 wird auf das Äußere des
Einheitskreises abgebildet. 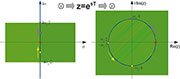
|
| Bild 72: So bildet sich die s-Ebene über die Transformation z = esT auf die z-Ebene ab. |
Setzt
man Gleichung (107) in Gleichung (105) ein, ergibt sich die
Definitionsformel für die einseitige z-Transformierte (Gleichung [108]).
Dabei wurden die Schreibvereinfachungen x(nTs) = x(n) und Xs(z) = X(z)
verwendet. 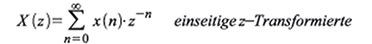
|
| Gleichung 108 |
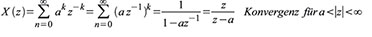
|
| Gleichung 109 |

|
| Gleichung 110 |
Tabelle 3 zeigt einige wichtige Korrespondenzen für die Laplace- und die z-Transformation. 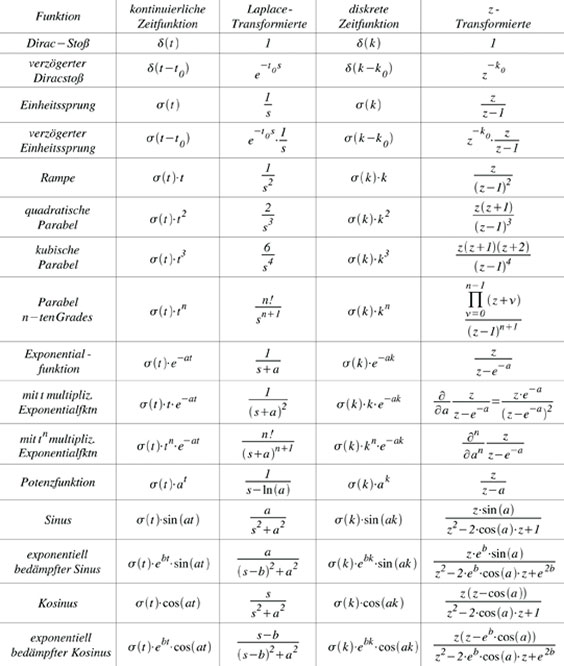
|
| Tabelle 3: Laplace- und z-Korrespondenzen |
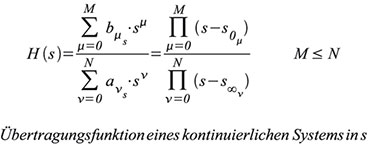
An
einem weiteren Beispiel wollen wir die Auswirkungen der Transformation
einer im s-Bereich gegebenen komplexen Übertragungsfunktion H(s) =
U2(s)/U1(s) in den z-Bereich studieren. Wir gehen davon aus, dass das
zugrunde liegende System linear und zeitinvariant ist (LTI-System). Dann
lässt sich seine Übertragungsfunktion als Quotient zweier Polynome in s
(Zählergrad ≤ Nennergrad) darstellen. Abbildung 70 stellt den Betrag
einer solchen Übertragungsfunktion mit Bandbegrenzung bei ±ωs/2 dar. 
|
| Gleichung 111 |
Die Übertragungsfunktion mit der Variablen s zeigt Gleichung (111).
- Die Nullstellen des Zählerpolynoms sind die Nullstellen der Übertragungsfunktion.
- Die Nullstellen des Nennerpolynoms bezeichnet man als Pole der Übertragungsfunktion, weil diese hier den Wert ∞ annimmt.
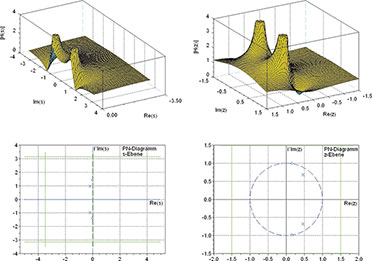
|
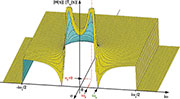
| Bild
73: Das Spektrum einer kontinuierlichen biquadratischen
Übertragungsfunktion im s-Bereich (oben links) und ihr PN-Diagramm
(unten links). Auf der rechten Seite die dreidimensionale Darstellung
des Abtastspektrums im z-Bereich (oben rechts) und die zugehörige
PN-Anordnung (unten rechts). |

|
| Gleichung 112 |

|
| Gleichung 113 |

|
| Gleichung 114 |
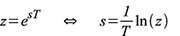
|
| Gleichung 115 |
Nun
wäre noch zu klären, wie der Betragsfrequenzgang von H(z) zu gewinnen
ist. Wir erinnern uns, dass die imaginäre Achse der komplexen s-Ebene
zwischen –ωs/2 < ω < ωs/2 auf den Einheitskreis in der z-Ebene
abgebildet wird (vergl. Abbildung 72). Deshalb müssen wir in Abbildung
73 oben rechts die Werte finden, deren Koordinaten in der z-Ebene einen
Abstand von 1 zum Ursprung aufweisen (|z| = 1). Am einfachsten kann man
dies tun, indem wir alle Werte von |H(z)| gleich null setzen, für die
|z| > 1 gilt. So stanzt man gewissermaßen den Teil von |H(z)| aus,
der innerhalb des Einheitskreises liegt. 
|
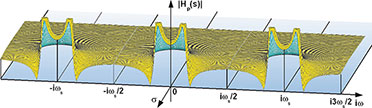
| Bild
74: Stanzt man das dreidimensionale Betragsspektrum der
Übertragungsfunktion in z im Abstand eins zum Ursprung der z-Ebene aus,
lässt sich an der Stanzkontur der Frequenzgang ablesen. |
Vertiefung
Bei
jedem LTI-System ist das Verhältnis zwischen Ausgangsgröße U2
(Reaktion) und Eingangsgröße U1 (Anregung) als Quotient zweier Polynome
in s oder z darstellbar. Man nennt diesen Quotienten die komplexe
Übertragungsfunktion des LTI-Systems in der Gestalt einer gebrochen
rationalen Funktion in s oder z. Die Nullstellen des Zählerpolynoms sind
die Nullstellen der Übertragungsfunktion, die Nullstellen des
Nennerpolynoms seine Pole.Ein
Polynom vom Grad n hat die allgemeine Gestalt gemäß Gleichung (116). Es
hat n Nullstellen (Wurzeln), d. h. es gibt n Werte für x, an denen y
den Wert null annimmt. Bei Polynomen mit reellen Koeffizienten hat jede
komplexe Wurzel x01 ein konjugiert komplexes Gegenstück x02, was
Gleichung (117) vermitteln soll. Reelle und komplexe Wurzeln können auch
jeweils in einer gewissen Vielfachheit auftreten. Weil sich jedes
Polynom durch seine Wurzeln in Form eines Produkts von Linearfaktoren
darstellen lässt, gilt: Gleichung (116) = Gleichung (118). 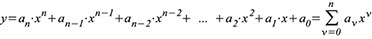
|
| Gleichung 116 |

|
| Gleichung 117 |
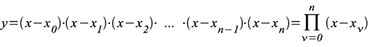
|
| Gleichung 118 |
Beispiel 1:
Die reellen Wurzeln 1, 2, 3, 4 führen zu Gleichung (119).
Beispiel 2:
Die konjugiert komplexen Wurzeln 1 ± i2 und 3 ± i4 sowie die relle Wurzel 5 führen zu Gleichung (120).
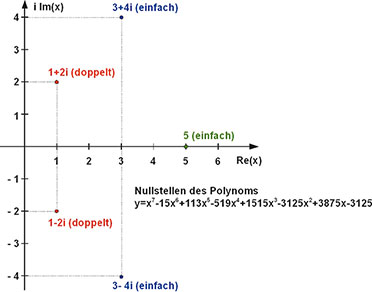
Beispiel 3:
Die
doppelten konjugiert komplexen Wurzeln 1 ± i2 und die einfache
konjugiert komplexe Wurzel 3 ± i4 sowie die relle Wurzel 5 führen zu
Gleichung (121).
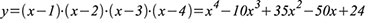
|
| Gleichung 119 |
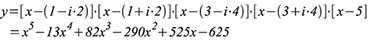
|
| Gleichung 120 |
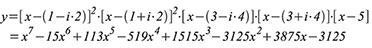
|
| Gleichung 121 |
|
| Bild 75: Ein Beispiel für den Zusammenhang zwischen der Koeffizientendarstellung eines Polynoms und dessen Nullstellen. |
|
| Gleichung 122 |

|
| Gleichung 123 |
Fachbeitrag als PDF-Download herunterladen
Inhalt
Sie erhalten den Artikel in 1 Version:
 als PDF (5 Seiten)
als PDF (5 Seiten)
Sie erhalten folgende Artikel:
- Einführung in die digitale Signalverarbeitung Teil 8/8
| weitere Fachbeiträge | Foren | |
Hinterlassen Sie einen Kommentar:






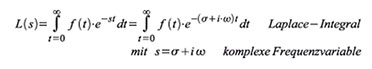

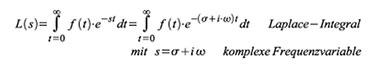
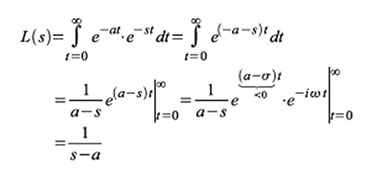

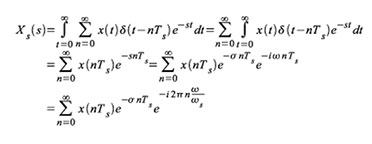
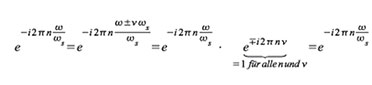



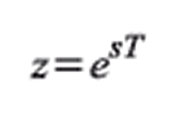

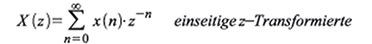
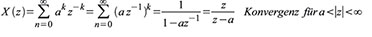







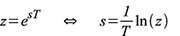

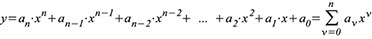

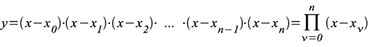
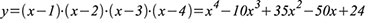
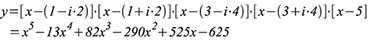
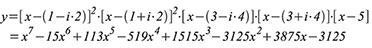



 als PDF (5 Seiten)
als PDF (5 Seiten)