1. Spannung, Stromstärke, Widerstand |
|
Die Stromstärke I wird in Ampere [A] gemessen. Bei der Stromstärke von 1Ampere fließen in der Sekunde 6.1018 Elektronen (=6 000 000 000 000 000 000 Elektronen) durch einen Leiterquerschnitt.
|
Messung der Stromstärke:
|
Messgeräte für die Stromstärke heißen Amperemeter.
Bei der Messung der Stromstärke muss das Amperemeter immer in Serie (hintereinander) mit dem Verbraucher (Lämpchen) geschaltet werden, damit der Strom sowohl durch den Verbraucher als auch durch das Messgerät fließen muss. Amperemeter müssen einen möglichst geringen elektrischen Widerstand haben, damit sie den Stromkreis möglichst wenig beeinflussen. |
Kleine Einheiten der Stromstärke:
| 1A = 1 000 000 Mikroampere(m A) = 1 000 Milliampere(mA) | z.B.: |
7,8 mA = 0,0078 A |
| 1 000 mA = 1 A | 12,5 mA = 0,0125 A | |
| 1 000 m A = 1 mA | 315 mA = 0,315 A | |
| 1mA = 0,001 A | ||
| 1 m A = 0,000 001 A |
1.2 Die elektrische Spannung U
Die Spannung U wird in Volt [V] gemessen. Unter der Spannung U kann man sich die "Kraft" vorstellen, mit der die Elektronen durch die Leitung getrieben werden.
Beispiele: Taschenlampenbatterie 4,5V, Stromnetz 220 V, Autobatterie 12V
|
Messung der Spannung:
|
Messgeräte für die Spannung heißen Voltmeter. Bei der Messung der Spannung muss das Voltmeter immer parallel zum Verbraucher Lämpchen) geschaltet werden. Voltmeter müssen einen möglichst hohen elektrischen Widerstand haben, damit sie den Stromkreis möglichst wenig beeinflussen. |
Kleine Einheiten der Spannung:
| 1V = 1 000 000 Mikrovolt(m V) = 1 000 Millivolt(mV) | z.B.: |
3,2 mV = 0,0032 V |
| 1 000 mV = 1 V | 17,8 mV = 0,0178 V | |
| 1 000 m V = 1 mV | 428 mV = 0,428 V | |
| 1mV = 0,001 V | ||
| 1 m V = 0,000 001 V |
1.3 Die elektrische Widerstand R, Ohmsches Gesetz
Die elektrische Widerstand R wird in Ohm [W ]W ] gemessen. Der Widerstand R eines Leiters gibt an, ob durch diesen Leiter bei gleicher Spannung viel oder wenig Strom (=Stromstärke) fließt. Ein Leiter hat den Widerstand von 1 W , wenn bei einer angelegten Spannung von 1 V eine Stromstärke von 1 A fließt. Gute Leiter haben einen geringen Widerstand.
Ohmsches Gesetz:
Das Ohmsche Gesetz gibt die Beziehung zwischen Spannung, Stromstärke und Widerstand an.
|
|
|
|
Messung des Widerstandes:
| 1)
|
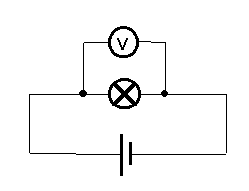 |
Durch Messung von
Spannung U und Stromstärke I (siehe !) kann mit Hilfe des Ohmschen
Gesetzes der Widerstand berechnet werden. |
| 2)
|
Mit einem Ohmmeter kann der elektrische Widerstand eines Verbrauchers direkt gemessen werden. Am zu messenden Verbraucher darf dabei keine Fremdspannung anliegen. Das Ohmmeter ist eine Spannungsquelle, die Größe der auftretenden Stromstärke ist ein Maß für den Widerstand, die Anzeige erfolgt in Ohm. |
Große Einheiten des elektrischen Widerstandes:
| 1 Megaohm (MW ) = 1 000 Kiloohm (kW ) = 1 000 000 Ohm (W ) | z.B.: |
1,2 kW ) = 1 200 W |
| 1 kW = 1000 W | 1,5 MW = 1 500 000 W |
1.4 Übungen
1) Spannungsmessung:
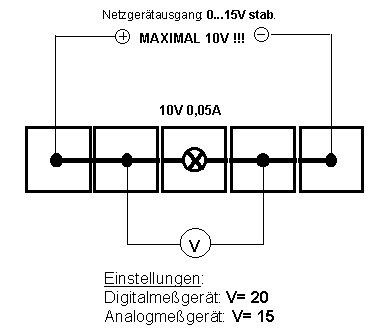 |
Teste die Übereinstimmung des Voltmeters mit der Einstellung des Netzgerätes.
Variiere die Spannung des Netzgerätes von 0 bis 10 Volt in 2V-Schritten. |
2) Stromstärkemessung, Berechnung und Messung des Lampenwiderstandes:
a)Berechnung des Lampenwiderstandes:
|
Variiere die Spannung am Netzgerät von 2V in 2V-Schritten bis 10 V.
Lies die eingestellte Spannung am Netzgerät, die daraus resultierende Stromstärke am Aperemeter ab.
Trage die so erhaltenen Werte in untenstehende Tabelle ein und berechne auch jeweils den Widerstand R.
|
|||||||||||||||
Netzgerät à |
U(V) |
2 |
4 |
6 |
8 |
10 |
||||||||||
Amperemeter à |
I(mA) |
|||||||||||||||
Amperemeter à |
I(A) |
|||||||||||||||
Berechnung à |
R(W ) |
|||||||||||||||
| I) Ergibt sich ein konstanter Wert für den Widerstand R der Lampe ? | ||||||||||||||||
| II) Wovon könnten die verschiedenen Widerstandswerte der Lampe abhängen ? | ||||||||||||||||
| b) | Messung des Lampenwiderstandes: | ||||||||||||||
|
Führe die Messung des Widerstandes R sowohl mit dem Digitalmeßgerät als auch mit dem Analogmeßgerät durch ! |
||||||||||||||
| I) | Das Digitalmeßgerät liefert den Widerstandswert: R = ..............W | ||||||||||||||
| II) | Das Analogmeßgerät liefert den Widerstandswert: R = ..............W | ||||||||||||||
III) |
Warum liefern diese beiden Meßgeräte völlig verschiedene Widerstandswerte für dieselben Glühbirne ? | ||||||||||||||
| Zusammenfassung: Die Glühlampe ist KEIN Ohmscher Widerstand. Ihr Widerstand wird mit steigender Temperatur (= mit steigender Stromstärke I) größer. Man sagt, sie hat einen positiven Temperaturkoeffizienten.
|
|||||||||||||||
| 3) Ermittle mit dem
Ohmmeter den Widerstand eines Bleistiftstriches:
|
|||||||||||||||
|
Zeichne einen dicken Bleistiftstrich auf ein Blatt weißes Papier.
Führe die Messung des Widerstandes R sowohl mit dem Digitalmeßgerät als auch mit dem Analogmeßgerät durch !
|
||||||||||||||
| I) | Das Digitalmeßgerät liefert den Widerstandswert: R = ..............W | ||||||||||||||
| II) | Das Analogmeßgerät liefert den Widerstandswert: R = ..............W | ||||||||||||||
| III) | Liefern beide Meßgeräte ca. denselben Widerstandswert ? | ||||||||||||||
| Zusammenfassung: Ein Bleistiftstrich verhält sich wie ein Ohmscher Widerstand. Er hat einen bestimmten Widerstandswert, der sich mit der Temperatur so gut wie nicht verändert.
|
|||||||||||||||
| 4) Hintereinanderschaltung
(Serienschaltung) von Widerständen:
|
|||||||||||||||
|
Baue nebenstehende Schaltung auf, variiere die Spannung U von 2V bis 12V (2V-Schritte) und miss dabei die in der folgenden Tabelle angeführten Größen: U, I, U1 und U2.
Bereche jeweils die Werte für U1+U2 und R !!
Versuche durch "geschicktes Umstecken" während der Messung, mit nur einem Messgerät auszukommen |
||||||||||||||
U |
I |
U1 |
U2 |
U1 + U2 |
R |
||||||||||
2 |
|||||||||||||||
4 |
|||||||||||||||
6 |
|||||||||||||||
8 |
|||||||||||||||
10 |
|||||||||||||||
12 |
|||||||||||||||
| I) | Durch welchen Widerstand fließt mehr Strom ? .................................................................. | ||||||||||||||
| II) | Welchen Wert ergibt die Summe der Teilspannungen U1+U2 ? .......................................... | ||||||||||||||
| III) | Wie verhalten sich die
beiden Teilspannungen U1 und U2 zueinander ?
............................ (Beachte besonders jene beiden Zeilen der Tabelle, in denen U=6V und U=12V und vergleiche mit den beiden Werten von R1 und R2 !) |
||||||||||||||
| IV) | Wie könnte man den Gesamtwiderstand R ohne Messung berechnen ? .......................... | ||||||||||||||
| Zusammenfassung: | Für die Hintereinanderschaltung (Serienschaltung) von Widerständen gilt: | ||||||||||||||
| Gesamtwiderstand: | R = R1 +R2 |
||||||||||||||
| Auftretende Stromstärken: | I = I1 = I2 |
||||||||||||||
| Auftretende Spannungen: | U = U1 + U2 |
||||||||||||||
| "Vermutung:" | U1 : U2 = R1 : R2 |
||||||||||||||
| 5) Nebeneinanderschaltung
(Parallelschaltung) von Widerständen:
|
||||||||||||||||
|
Baue nebenstehende Schaltung auf, variiere die Spannung U von 2V bis 12V (2V-Schritte) und miss dabei die in der folgenden Tabelle angeführten Größen: U, I, I1 und I2.
Bereche jeweils die Werte für I1 + I2 und R !!
Versuche mit einem Messgerät auszukommen. |
|||||||||||||||
U |
I |
I1 |
I2 |
I1 + I2 |
R |
|||||||||||
2 |
||||||||||||||||
4 |
||||||||||||||||
6 |
||||||||||||||||
8 |
||||||||||||||||
10 |
||||||||||||||||
12 |
||||||||||||||||
| I) | Durch welchen Widerstand fließt mehr Strom ? ................................................................. | |||||||||||||||
| II) | An welchem Widerstand liegt die größere Spannung ? ..................................................... | |||||||||||||||
| III) | Welchen Wert ergibt die Summe der Teilströme I1 + I2 ? .................................................... | |||||||||||||||
| IV) | Wie könnte man den Gesamtwiderstand R ohne Messung berechnen ? ......................... | |||||||||||||||
| Zusammenfassung: | Für die Nebeneinanderschaltung (Parallelschaltung) von Widerständen gilt: | |||||||||||||||
| Gesamtwiderstand: |
|
|||||||||||||||
| Auftretende Stromstärken: | I = I1 + I2 |
|||||||||||||||
| Auftretende Spannungen: | U = U1 = U2 |
|||||||||||||||
| 6) Spannungsteiler:
|
||||||||||||||||
| a) | Fester Spannungsteiler: | |||||||||||||||
|
Baue nebenstehende Schaltung auf und stelle die Spannung U einmal genau auf 6V und einmal genau auf 12V ein.
Miß in beiden Fällen die Werte für U1 und U2 und trage sie in untenstehende Tabelle ein und berechne jeweils U1 + U2 !
|
|||||||||||||||
| I) | Wie verhalten sich die beiden Spannungen U1 und U2 zueinander ? ............................ | |||||||||
| II) | Hängt das Verhältnis U1 : U2 von der angelegten Spannung U ab ? ........................... | |||||||||
| III) | Welchen Wert liefert jeweils die Summe U1+U2 ? .......................................................... | |||||||||
| Zusammenfassung: | I) | Betrachtung für U=8V: | ||||||||
| R = R1 + R2 | ||||||||||
| R = 100W + 500W | ||||||||||
| R = 600W | ||||||||||
| U1 = I . R1 = 0,02 . 100 = 2V | ||||||||||
| U2 = I . R2 = 0,02 . 500 = 10V | ||||||||||
| Die angelegte Spannung U=12V wird somit in 2V und 10V geteilt. | ||||||||||
| II) | U1 : U2 verhält sich wie R1 : R2, also wie 100 : 500 = 1 : 5. | |||||||||
| III) | Die Summe der Teilspannungen U1+U2 ergibt die angelegte Spannung U. | |||||||||
| b) | Variabler Spannungsteiler: | |||||||||
|
Baue nebenstehende Schaltung auf und stelle die Spannung U genau auf 10V ein.
Variiere den Wert des verstellbaren Widerstandes von 0W bis 10kW . Miß dabei die Werte für U1 und U2 und trage sie in untenstehende Tabelle ein und berechne jeweils U1 + U2 !
|
|||||||||
| I) | Welche Spannungswerte kann U1 durch Variation von R1 erreichen ? ......................... | |||||||||
| II) | Welche Spannungswerte resultieren daraus für U2 ? ..................................................... | |||||||||
| III) | Welchen Wert liefert jeweils die Summe U1+U2 ? .......................................................... | |||||||||
| Zusammenfassung: | I) | Durch
Variation von R1 nimmt U1 JEDEN Wert zwischen 0
Volt und 5 Volt an ! U2 geht von 10 Volt bis 5 Volt.
|
||||||||
| II) | Die
Teilspannungen verhalten sich immer wie die Widerstände: U1 : U2 = R1 : R2
|
|||||||||
| III) | Die Summe
der Teilspannungen ergibt immer die angelegte Spannung U: U1 + U2 = U |
|||||||||