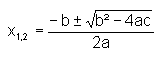Mathias BORG 5a Mathematik: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (13 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== Mathematik Klasse | Diese Seite gehört {{Mathias}} und ist Teil von [[Mathias Schule]], [[Mathias Schuljahr 2019/2020 5a BORG Neulengbach]]. | ||
== Mathematik Klasse 5a - 2019/2020 - Mathias Scherer == | |||
=== Thema: xxx === | === Thema: xxx === | ||
| Zeile 9: | Zeile 11: | ||
* 3. Form: (a+b)(a-b) = a**2 -b**2 | * 3. Form: (a+b)(a-b) = a**2 -b**2 | ||
=== Thema: | === Thema: Terme === | ||
Noch zu ergänzen: | |||
* Was sind Terme? | |||
* Was muss ich darüber wissen? | |||
=== Thema: quadratische Gleichungen === | === Thema: quadratische Gleichungen === | ||
| Zeile 16: | Zeile 21: | ||
* "große Formel" / abc-Formel | * "große Formel" / abc-Formel | ||
*: <code>x(1,2) = (-b +- SQRT(b**2 - 4*a*c)) / (2a) </code> | |||
*: [[Datei:Formelnb3.gif]] | |||
* "kleine Formel" / pq-Formel | * "kleine Formel" / pq-Formel | ||
* Satz von Vieta | * Satz von Vieta | ||
=== Thema: Gleichungssystem in 2 | === Thema: Gleichungssystem in 2 Unbekannten === | ||
==== Lösungs-Vorgehen: "Gleichsetzung" ==== | ==== Lösungs-Vorgehen: "Gleichsetzung" ==== | ||
| Zeile 27: | Zeile 34: | ||
# wie geht man vor? | # wie geht man vor? | ||
## beide Gleichungen nach derselben Unbekannten auflösen | ## beide Gleichungen nach derselben Unbekannten auflösen | ||
## die Lösungs-Ergebnisse in Form einer Gleichung (die nun nur mehr in einer Unbekannten ist) aufschreiben und lösen (durch Umformung, etc.) | ## die Lösungs-Ergebnisse in Form einer Gleichung (die nun nur mehr in '''einer''' Unbekannten ist) aufschreiben und lösen (durch Umformung, etc.) | ||
## die 2. Unbekannte durch einsetzen in eine der beiden aufgelösten | ## die 2. Unbekannte durch einsetzen in eine der beiden aufgelösten Teil-Gleichungen aus Schritt 1 ermitteln | ||
## Die Probe machen, indem die Lösungswerte in die beiden Ursprungs- | ## Die Probe machen, indem die Lösungswerte in die beiden Ursprungs-Gleichungen eingesetzt werden | ||
===== Textbeispiel 1 ===== | |||
Aufgabe: Ich bin 3 Jahre jünger als mein Bruder und mein Bruder ist doppelt so alt wie ich. Wie alt sind wir beide? | |||
<pre> | |||
i+3=b | |||
i*2=b | |||
i+3=i*2 | -3 | |||
i=i*2-3 | -i | |||
0=i-3 | +3 | |||
3=i | |||
b=3+3 | |||
b=3*2 | |||
b=6 | |||
3+3=6 | |||
3*2=6 | |||
</pre> | |||
Aktuelle Version vom 24. Jänner 2020, 13:29 Uhr
Diese Seite gehört Mathias und ist Teil von Mathias Schule, Mathias Schuljahr 2019/2020 5a BORG Neulengbach.
Mathematik Klasse 5a - 2019/2020 - Mathias Scherer
Thema: xxx
Thema: binomische Formeln
- 1. Form: (a+b)**2 = a**2 + 2ab + b**2
- 2. Form: (a-b)**2 = a**2 - 2ab + b**2
- 3. Form: (a+b)(a-b) = a**2 -b**2
Thema: Terme
Noch zu ergänzen:
- Was sind Terme?
- Was muss ich darüber wissen?
Thema: quadratische Gleichungen
Lösungs-Vorgehens-Varianten
- "große Formel" / abc-Formel
- "kleine Formel" / pq-Formel
- Satz von Vieta
Thema: Gleichungssystem in 2 Unbekannten
Lösungs-Vorgehen: "Gleichsetzung"
- was ist die Essenz davon?
- ....
- wie geht man vor?
- beide Gleichungen nach derselben Unbekannten auflösen
- die Lösungs-Ergebnisse in Form einer Gleichung (die nun nur mehr in einer Unbekannten ist) aufschreiben und lösen (durch Umformung, etc.)
- die 2. Unbekannte durch einsetzen in eine der beiden aufgelösten Teil-Gleichungen aus Schritt 1 ermitteln
- Die Probe machen, indem die Lösungswerte in die beiden Ursprungs-Gleichungen eingesetzt werden
Textbeispiel 1
Aufgabe: Ich bin 3 Jahre jünger als mein Bruder und mein Bruder ist doppelt so alt wie ich. Wie alt sind wir beide?
i+3=b i*2=b i+3=i*2 | -3 i=i*2-3 | -i 0=i-3 | +3 3=i b=3+3 b=3*2 b=6 3+3=6 3*2=6